《2025年通城学典暑期升级训练延边大学出版社八年级数学华师大版》

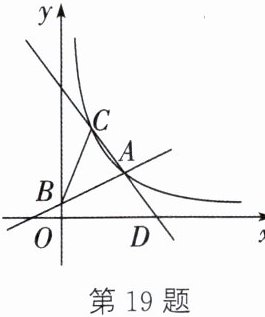
19.(14分)(济南中考)如图,一次函数$y= \frac {1}{2}x+1的图象与反比例函数y= \frac {k}{x}(x＞0)的图象交于点A(a,3)$,与y轴交于点B.
(1)求a、k的值.
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,$AC= AD$,连结CB.
① 求$\triangle ABC$的面积；
② 点P在反比例函数的图象上,点Q在x轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.

答案： （1）把$ A(a,3) $代入$ y = \frac{1}{2}x + 1 $，得$ \frac{1}{2}a + 1 = 3 $，解得$ a = 4 $.$ \therefore A(4,3) $.把$ A(4,3) $代入$ y = \frac{k}{x} $，得$ 3 = \frac{k}{4} $，解得$ k = 12 $.（2）①$ \because $点$ A $的坐标是$ (4,3) $，点$ D $的纵坐标是0，$ AC = AD $，$ \therefore $易得点$ C $的纵坐标是$ 3×2 - 0 = 6 $.把$ y = 6 $代入$ y = \frac{12}{x} $，得$ x = 2 $，$ \therefore C(2,6) $.过点$ C $作$ CM\perp x $轴于点$ M $，交$ AB $于点$ E $.在$ y = \frac{1}{2}x + 1 $中，当$ x = 2 $时，$ y = \frac{1}{2}×2 + 1 = 2 $，$ \therefore E(2,2) $.$ \because C(2,6) $，$ \therefore CE = 6 - 2 = 4 $.$ \therefore S_{\triangle ABC}=\frac{1}{2}CE\cdot|x_{A}|=\frac{1}{2}×4×4 = 8 $.②设点$ P $的坐标为$ (x_{P},y_{P}) $.当$ AB $是对角线，即四边形$ APBQ $是平行四边形时，$ \because A(4,3) $，$ B(0,1) $，点$ Q $的纵坐标为0，$ \therefore y_{P}=1 + 3 - 0 = 4 $.在$ y = \frac{12}{x} $中，当$ y = 4 $时，$ 4 = \frac{12}{x} $，解得$ x = 3 $.$ \therefore P(3,4) $；当$ AB $为边，即四边形$ ABQP $是平行四边形时，由$ y_{Q}-y_{B}=y_{P}-y_{A} $，得$ 0 - 1 = y_{P}-3 $，$ \therefore y_{P}=2 $.在$ y = \frac{12}{x} $中，当$ y = 2 $时，$ 2 = \frac{12}{x} $，解得$ x = 6 $.$ \therefore P(6,2) $.综上所述，点$ P $的坐标为$ (3,4) $或$ (6,2) $.

20.(15分)$∠QPN$的顶点P在正方形ABCD两条对角线的交点处,$∠QPN= α$,将$∠QPN$绕点P旋转,旋转过程中$∠QPN$的两边分别与正方形ABCD的边AD和CD交于点E、F(点F不与点C、D重合).
(1)如图①,当$α=90^{\circ }$时,DE、DF、AD之间满足的数量关系是____；
(2)如图②,将图①中的正方形ABCD改为$∠ADC= 120^{\circ }$的菱形,其他条件不变,当$α=60^{\circ }$时,求证：$DE+DF= \frac {1}{2}AD$；
(3)在(2)的条件下,若旋转过程中$∠QPN$的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE、DF、AD之间满足的数量关系,直接写出结论,不用加以证明.

答案：
（1）$ DE + DF = AD $.（2）如图①，取$ AD $的中点$ M $，连结$ PM $，则$ AM = DM $.$ \because $四边形$ ABCD $为菱形，$ \angle ADC = 120^{\circ} $，$ \therefore CD = AD $，$ \angle DAP = 30^{\circ} $，$ AC\perp BD $，$ \angle ADP = \angle CDP = 60^{\circ} $.在$ \text{Rt}\triangle APD $中，$ \because AM = DM $，$ \therefore PM = DM $.$ \therefore \triangle MDP $是等边三角形.$ \therefore PM = PD $，$ \angle MPD = 60^{\circ} $，$ \angle PME = \angle PDF = 60^{\circ} $.$ \because \angle QPN = 60^{\circ} $，$ \therefore \angle MPD - \angle QPD = \angle QPN - \angle QPD $，即$ \angle MPE = \angle DPF $.在$ \triangle MPE $和$ \triangle DPF $中，$ \begin{cases} \angle PME=\angle PDF, \\ PM=PD, \\ \angle MPE=\angle DPF, \end{cases} $$ \therefore \triangle MPE\cong \triangle DPF $.$ \therefore ME = DF $.$ \therefore DE + DF = DE + ME = DM = \frac{1}{2}AD $.（3）在整个运动变化过程中，①如图①，当点$ E $落在$ AD $上时，$ DE + DF = \frac{1}{2}AD $；②如图②，当点$ E $落在$ AD $的延长线上时，$ DF - DE = \frac{1}{2}AD $.