《2025年通城学典暑期升级训练延边大学出版社八年级数学华师大版》

10. 若点$A(1,y_{1})$、$B(-2,y_{2})$、$C(-3,y_{3})都在反比例函数y= \frac {6}{x}$的图象上,则$y_{1}$、$y_{2}$、$y_{3}$的大小关系是____.(用“＜”连接)

答案： $y_{2}＜y_{3}＜y_{1}$

11. 分式方程$\frac {3}{x+2}-\frac {1}{x}= \frac {4}{x^{2}+2x}$的解为____.

答案： $x = 3$

12.(辽宁中考)如图,在$\triangle ABC$中,$AB= AC$,$∠B= 54^{\circ }$,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于$\frac {1}{2}AD$长为半径作弧,两弧相交于点E,作直线CE,交AB于点F,则$∠ACF$的度数是____.

答案： $18^{\circ}$

13. 葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱,那么它的底面周长是12dm.当一段葛藤绕树干盘旋1圈升高9dm时,这段葛藤的长是____dm.

答案： 15

14. 如图,在平面直角坐标系内,矩形OABC的顶点O位于坐标原点,点A的坐标为$(2,0)$,点C的坐标
答案讲解
为$(0,4)$,点D和点E分别位于线段AC、AB上,将$\triangle ABC$沿DE折叠,恰好能使点A与点C重合.若x轴上有一点P,能使$\triangle AEP$为等腰三角形,则点P的坐标为____.

答案： $ \left(-\frac{1}{2},0\right) $或$ \left(\frac{9}{2},0\right) $

15.(12分)
(1)计算：$(2x+3)^{2}-4x(3-x)$；
(2)先化简,再求值：$(\frac {a^{2}+a-1}{a+2}-\frac {a}{2+a})÷\frac {a^{2}-1}{a}-1$,其中$a= 2$.

答案： （1）$ 8x^{2}+9 $.（2）原式$ =-\frac{2}{a+2} $.当$ a = 2 $时，原式$ =-\frac{2}{2+2}=-\frac{1}{2} $.

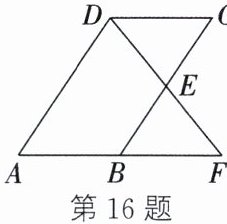
16.(9分)如图,在$□ ABCD$中,E是BC的中点,连结DE并延长,交AB的延长线于点F.求证：$AB= BF$.

答案： $ \because E $是$ BC $的中点，$ \therefore CE = BE $.$ \because $四边形$ ABCD $是平行四边形，$ \therefore AB// CD $，$ AB = CD $.$ \therefore \angle DCE = \angle FBE $.在$ \triangle CED $和$ \triangle BEF $中，$ \begin{cases} \angle DCE=\angle FBE, \\ CE=BE, \\ \angle CED=\angle BEF, \end{cases} $$ \therefore \triangle CED\cong \triangle BEF $.$ \therefore CD = BF $.$ \therefore AB = BF $.