《2025年通城学典暑期升级训练延边大学出版社八年级数学华师大版》

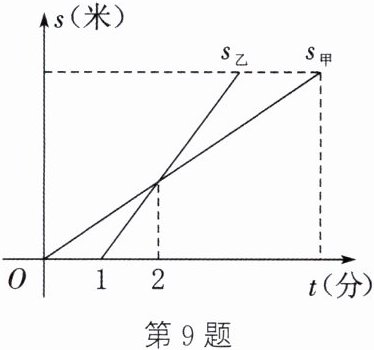
9. (巴中中考)甲、乙两人沿同一直道从A地到B地,在整个行程中,甲、乙离A地的距离s(米)与时间t(分)之间的函数关系如图所示.下列说法中,错误的是( )

A.甲比乙早1分钟出发
B.乙的速度是甲的2倍
C.若甲比乙晚5分钟到达,则甲用时10分钟
D.若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达B地

答案： C

10. 若双曲线$y= \frac{m - 1}{x}$在每个象限内,函数值y随x的增大而减小,则m的取值范围是______.

答案： m＞1

11. 地面温度为$15^{\circ}C$,若高度每升高1km,气温下降$6^{\circ}C$,则高度h(km)与气温$t(^{\circ}C)$之间的函数表达式为______.

答案： h=$\frac{15−t}{6}$

12. 某网约车平台收费y(元)与所行驶的路程x(千米)之间的函数关系如图所示.小明乘坐该平台的网约车从家到机场共花费64元.若车速始终保持60千米/时,不考虑其他因素(红绿灯、堵车等),则他从家到机场需要______分钟.

答案： 20

13. (东营中考)如图,$\triangle OAB$是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数$y= \frac{1}{x}(x\gt0)$的图象上,则经过点A的反比例函数图象对应的表达式为______.

答案：
y=−$\frac{1}{x}$(x＜0) 解析:如图,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,则∠ADO=∠BCO=90°.
∴∠AOD+∠OAD=90°.又
∵△OAB是等腰直角三角形,
∴∠AOB=90°.
∴∠AOD+∠BOC=90°.
∴∠BOC=∠OAD.又
∵OB=OA,
∴△BOC≌△OAD.
∵点B在反比例函数y=$\frac{1}{x}$(x＞0)的图象上，
∴易得$S_{\triangle OBC}=\frac{1}{2}$.设经过点A的反比例函数图象对应的表达式为y=$\frac{k}{x}$(x＜0).
∵$S_{\triangle OAD}=S_{\triangle OBC}=\frac{1}{2}$，
∴易得k=−1.
∴经过点A的反比例函数图象对应的表达式为y=−$\frac{1}{x}$(x＜0).

14. 如图,在平面直角坐标系中,正方形$OA_{1}B_{1}C_{1}$、$C_{1}A_{2}B_{2}C_{2}$、$C_{2}A_{3}B_{3}C_{3}$、…、$C_{n - 1}A_{n}B_{n}C_{n}的顶点A_{1}$、$A_{2}$、$A_{3}$、…、$A_{n}在直线y = kx + b$上,顶点$C_{1}$、$C_{2}$、$C_{3}$、…、$C_{n}$在x轴上.已知点$B_{1}的坐标为(1,1)$,点$B_{2}的坐标为(3,2)$,则点$A_{n}$的坐标为______.

答案： ($2^{n - 1}-1$,$2^{n - 1}$) 解析:
∵点$B_1$的坐标为(1,1)，点$B_2$的坐标为(3,2)，
∴正方形$OA_1B_1C_1$的边长为1，正方形$C_1A_2B_2C_2$的边长为2.
∴点$A_1$的坐标为(0,1)，点$A_2$的坐标为(1,2).把$A_1(0,1)$、$A_2(1,2)$代入y=kx+b，得$\begin{cases}b = 1, \\k + b = 2,\end{cases}$解得$\begin{cases}b = 1, \\k = 1.\end{cases}$
∴直线y=kx+b对应的函数表达式为y=x+1.由题意，易知点$A_1$的纵坐标为1=$2^0$，点$A_1$的横坐标为0=$2^0 - 1$；点$A_2$的纵坐标为1 + 1=$2^1$，点$A_2$的横坐标为1=$2^1 - 1$；点$A_3$的纵坐标为2 + 2 = 4=$2^2$，点$A_3$的横坐标为1 + 2 = 3=$2^2 - 1$；点$A_4$的纵坐标为4 + 4 = 8=$2^3$，点$A_4$的横坐标为1 + 2 + 4 = 7=$2^3 - 1$……据此可以得到点$A_n$的坐标为($2^{n - 1}-1$,$2^{n - 1}$).

15. (6分)已知y与$2x - 1$成正比例,当$x = 3$时,$y = 10$.
(1)求y与x之间的函数表达式；
(2)当$y = 2$时,求x的值.

答案： （1）由题意，设y与x之间的函数表达式为y=k(2x - 1).
∵当x = 3时，y = 10，
∴10 = k(6 - 1)，解得k = 2.
∴y与x之间的函数表达式为y = 2(2x - 1)=4x - 2.（2）由（1）知，y与x之间的函数表达式为y = 4x - 2，
∴当y = 2时，2 = 4x - 2，解得x = 1.