《2025年通城学典暑期升级训练延边大学出版社八年级数学华师大版》

12. 新情境 日常生活(青岛中考)某校举办了以"强体质,炼意志"为主题的体育节.小亮报名参加3000米比赛项目,经过一段时间的训练,比赛时小亮的平均速度比训练前提高了25%,跑完全程少用了3分钟.设小亮训练前的平均速度为x米/分,则x满足的分式方程为____.

答案： $\frac{3000}{x}-\frac{3000}{(1+25\%)x}=3$

13. 若关于x的分式方程$\frac{x}{x - 2} - m = \frac{2m}{2 - x}$无解,则m的值为____.

答案： 1或-1 解析:方程$\frac{x}{x-2}-m=\frac{2m}{2-x}$两边同时乘以$(x-2)$,得$x-m(x-2)=-2m$.整理,得$(1-m)x=-4m$.分两种情况讨论:当$x-2≠0$时,方程无解.$\therefore 1-m=0.\therefore m=1$.当$x-2=0$,即$x=2$时,方程无解.将$x=2$代入$(1-m)x=-4m$中,解得$m=-1$.综上所述,$m$的值为1或-1.

14. (8分)
(1)★解方程:$1 - \frac{2}{3 - x} = \frac{4}{x - 3}$;
(2)先化简,再求值:$(\frac{3}{x - 1} - x - 1) ÷ \frac{x^2 - 4x + 4}{x - 1}$,其中$x = 3$.

答案： （1）去分母,得$x-3+2=4$,解得$x=5$.当$x=5$时,$x-3≠0$,$\therefore x=5$是原方程的解.易错提示解分式方程容易忽略检验解分式方程在方程两边乘以同一个含未知数的整式，并约去了分母,可能会产生不适合原分式方程的解(根),即增根.因此解分式方程必须检验根,将所得的解代入最简公分母看是否为零即可判断,这点常常被忽略.（2）原式$=\frac{3-(x^{2}-1)}{x-1}\cdot \frac{x-1}{(x-2)^{2}}=\frac{(x+2)(x-2)}{x-1}\cdot \frac{x-1}{(x-2)^{2}}=\frac{-x+2}{x-2}$.当$x=3$时,原式$=\frac{-3+2}{3-2}=-5$.

15. (7分)某商家用6000元购进若干袋奶枣,很快售完,该商家又用9600元购进第二批这种奶枣,所进的数量是第一批的1.5倍,每袋奶枣的进价比第一批每袋奶枣的进价贵2元.该商家购进的第一批奶枣有多少袋?

答案： 设该商家购进的第一批奶枣有$x$袋,则购进的第二批奶枣有$1.5x$袋.由题意,得$\frac{6000}{x}+2=\frac{9600}{1.5x}$,解得$x=200$.经检验,$x=200$是原方程的解,且符合题意.$\therefore$该商家购进的第一批奶枣有200袋.

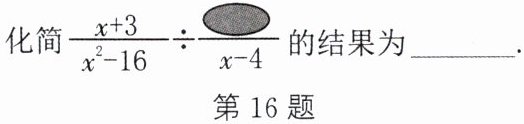
16. (7分)如图,作业本上有这样一道填空题,其中有一部分被墨水污染了,已知该题化简的结果为$\frac{1}{x + 4}$.
(1)求被墨水污染的部分.
(2)在(1)的条件下,原分式的值能等于$\frac{1}{8}$吗?请说明理由.

答案： （1）设被墨水污染的部分是$A$.由题意,得$\frac{x+3}{x^{2}-16}÷ \frac{A}{x-4}=\frac{1}{x+4}$,解得$A=x+3$.$\therefore$被墨水污染的部分为$x+3$.（2）不能.理由:若$\frac{1}{x+4}=\frac{1}{8}$,则$x=4$.$\because$当$x=4$时,$x^{2}-16=0$,原分式无意义,$\therefore$原分式的值不能等于$\frac{1}{8}$.

17. (8分)(舟山中考)观察下列等式:$\frac{1}{2} = \frac{1}{3} + \frac{1}{6},\frac{1}{3} = \frac{1}{4} + \frac{1}{12},\frac{1}{4} = \frac{1}{5} + \frac{1}{20},...$.
(1)按上面的规律归纳出一个一般的结论;(用含n的等式表示,n为正整数)
(2)请运用分式的有关知识,推理说明这个结论是正确的.

答案： （1）观察规律,可得$\frac{1}{n}=\frac{1}{n+1}+\frac{1}{n(n+1)}$.（2）$\because \frac{1}{n+1}+\frac{1}{n(n+1)}=\frac{n}{n(n+1)}+\frac{1}{n(n+1)}=\frac{n+1}{n(n+1)}=\frac{1}{n}$,$\therefore \frac{1}{n}=\frac{1}{n+1}+\frac{1}{n(n+1)}$是正确的.