《2025年通城学典暑期升级训练延边大学出版社八年级数学华师大版》

11. 如图,在矩形$ABCD$中,$AB = 5$,$AD = 12$.$P是AD边上不与点A和点D$重合的一个动点,过点$P分别作AC和BD$的垂线,垂足分别为$E$、$F$,则$PE + PF = $______.

答案： $\frac{60}{13}$

12. *如图,在矩形$ABCD$中,$AB = 4cm$,$AD = 12cm$,点$P从点A$出发,向点$D以1cm/s$的速度匀速运动,点$Q以4cm/s的速度从点C$出发,在$B$、$C$两点之间往返匀速运动,两点同时出发,点$P到达点D$时停止运动(同时点$Q$也停止运动).设运动时间为$t s$,这段时间内,当$t$的值为______时,以$P$、$Q$、$C$、$D$为顶点的四边形是矩形.

答案： 2.4或4或7.2 解析:根据题意，知当点P从点A运动到点D的过程中,点Q将按照C→B→C→B→C运动.
∵四边形ABCD是矩形，
∴AD//BC,∠D=90°.
∴PD//CQ.若DP=CQ,则四边形PDCQ是矩形.根据题意,得DP=(12−t)cm.当0≤t≤3时,CQ=4tcm,12−t=4t,解得t=2.4.当3＜t≤6时,CQ=(24−4t)cm,12−t=24−4t,解得t=4.当6＜t≤9时,CQ=(4t−24)cm,12−t=4t−24,解得t=7.2.当9＜t＜12 时,CQ=(48−4t)cm,12−t=48−4t,解得t=12,此时无法构成矩形,故舍去.综上所述，当t=2.4或4或7.2时，以P、Q、C、D为顶点的四边形是矩形.
易错提示
因对动点的位置考虑不全而丢解
与动点有关的问题,一定要注意考虑题目中涉及的情形是否是唯一的.如果情形不唯一,那么题目就有多个解.本题中因为点Q在B、C两点之间往返运动,所以表示线段CQ的长度的代数式是随着点Q的运动而变化的,因此要考虑全面,防止丢解.

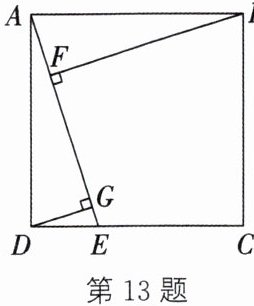
13.(10分)如图,四边形$ABCD$是正方形,$E是CD$边上任意一点,连结$AE$,作$BF⊥AE$,$DG⊥AE$,垂足分别为$F$、$G$.求证：$AF = DG$.

答案：
∵四边形ABCD是正方形,
∴AB=AD,∠DAB=90°.
∵BF⊥AE,DG⊥AE,
∴∠AFB=∠AGD=∠ADG+∠DAG=90°.
∵∠DAG+∠BAF=∠DAB=90°,
∴∠ADG=∠BAF.在△BAF和△ADG中,∠BAF=∠ADG,∠AFB=∠DGA,AB=DA,
∴△BAF≌△ADG.
∴AF=DG.

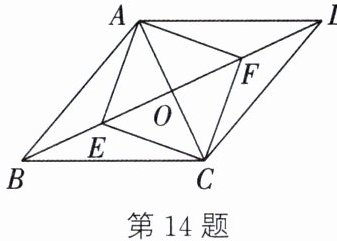
14.(10分)(邵阳中考)如图,在菱形$ABCD$中,对角线$AC$、$BD相交于点O$,点$E$、$F在对角线BD$上,且$BE = DF$,$OE = OA$.求证：四边形$AECF$是正方形.

答案：
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD.
∵BE=DF,
∴OB−BE=OD−DF,即OE=OF.
∴易得四边形AECF是菱形.
∵OE=OA=OF,AC⊥BD,
∴∠EAO=∠AEO=∠FAO=∠AFO=45°.
∴∠EAF=90°.
∴四边形AECF是正方形.

15.(12分)(舟山中考)小惠自编一题：如图,在四边形$ABCD$中,对角线$AC$、$BD相交于点O$,$AC⊥BD$,$OB = OD$.求证：四边形$ABCD$是菱形.她将自己的证明过程与同学小洁交流,如下表：
|小惠|小洁|
|证明：$\because AC⊥BD$,$OB = OD$,$\therefore AC垂直平分BD$.$\therefore AB = AD$,$CB = CD$.$\therefore四边形ABCD$是菱形.|这个题目还缺少条件,需要补充一个条件才能证明.|
若赞同小惠的证法,请在小惠的证法处画“√”；若赞成小洁的说法,请你补充一个条件,并证明.

答案： 赞成小洁的说法，补充的条件不唯一，如OA=OC.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.又
∵AC⊥BD,
∴四边形ABCD是菱形.