《2025年暑假衔接直通车五年级数学人教版》

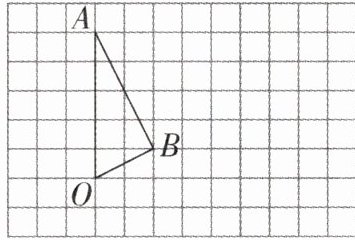
【典型例题】画出三角形 AOB 向右平移 4 格后的图形 $ A'O'B' $；再画出三角形 AOB 绕 O 点顺时针旋转 $ 90^{\circ} $后的图形,并在图中标出点 B 和点 C 的对应点 $ A'' $和 $ B'' $。

思路分析
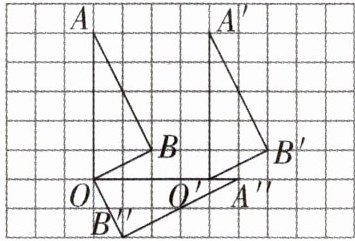
选定三角形 AOB 的 3 个顶点；把 3 个顶点 A、O、B 分别向右平移 4 格,得到对应点 $ A' $、$ O' $、$ B' $；根据三角形 AOB 的形状顺次连接平移后的对应点,即可得到平移后的三角形 $ A'O'B' $。
三角形 AOB 绕 O 点顺时针旋转 $ 90^{\circ} $,所以点 O 的位置不变。找出三角形 AOB 另外两个顶点 A、B 的位置；根据对应点旋转 $ 90^{\circ} $,对应线段长度不变找出顶点 A、B 旋转后的对应点 $ A'' $和 $ B'' $；顺次连接对应点,就能得到旋转后的三角形 $ A''OB'' $。
正确解答

答案：

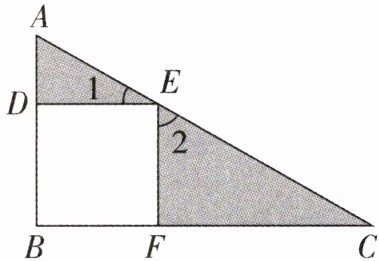
【典型例题】如图,四边形 DEFB 是一个正方形。在三角形 ABC 中,AE 长 4 cm,EC 长 8 cm。涂色部分的面积是多少平方厘米？

思路分析
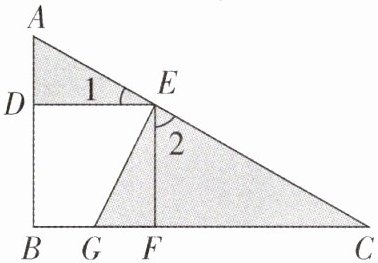
(1)以点 E 为旋转中心,三角形 ADE 绕点 E 逆时针旋转 $ 90^{\circ} $后,DE 和 FE 重合,在 FB 上截取 $ FG = DA $,连接 EG,三角形 GFE 就是三角形 ADE 绕点 E 逆时针旋转 $ 90^{\circ} $后的图形(如下图)。
(2)DEFB 是一个正方形,$ \angle DEF $是一个直角,则 $ \angle 1 $与 $ \angle 2 $的和为 $ 90^{\circ} $,图形旋转前后对应角的大小相等,$ \angle GEF = \angle 1 $,那么 $ \angle GEC = 90^{\circ} $,有一个角为直角的三角形是直角三角形。
(3)由图可知,$ AE = GE = 4 $cm,$ EC = 8 $cm,三角形 GEC 是直角三角形,利用“三角形的面积 = 底×高÷2”求出三角形 GEC 的面积就是阴影部分的面积,据此解答。
正确解答 $ 4×8÷2 = 16(cm^{2}) $

答：涂色部分的面积是 $ 16 cm^{2} $。

答案： 解析：本题考查图形旋转后利用直角三角形面积公式求解涂色部分面积的知识点，通过将三角形$ADE$旋转，构造出直角三角形$GEC$，再根据三角形面积公式计算其面积，该面积即为涂色部分面积。
答案：$4×8÷2 = 16(cm^{2})$
答：涂色部分的面积是$16cm^{2}$。