2025年暑假衔接直通车五年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接直通车五年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
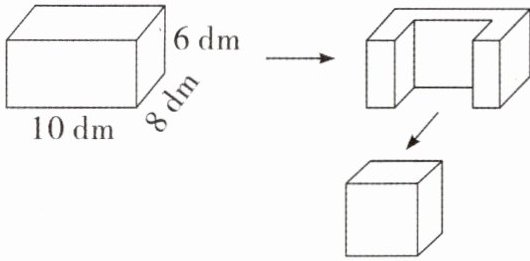
【典型例题】一个长方体,长 10 dm,宽 8 dm,高 6 dm。如图,从这个长方体中截去一个最大的正方体,剩下的部分的体积是多少立方分米?剩下的部分的表面积是多少平方分米?
思路分析
在这个长方体中截去一个最大的正方体,这个正方体的棱长对应长方体的高。(1)剩下部分的体积就等于长方体的体积减去棱长为 6 dm 的小正方体的体积,根据长方体的体积公式:$V = abh$,正方体的体积公式:$V = a^{3}$,把数据代入公式求出长方体与正方体的体积差即可。
(2)根据图形中的切割特点,剩下的部分的表面积比原来增加了边长为 6 dm 的 3 个正方形面的面积,同时减少了 3 个边长为 6 dm 的小正方形的面积,则剩下部分的表面积就等于原来长方体的表面积。
正确解答 $10×8×6 - 6×6×6 = 264(dm^{3})$
$(10×8 + 10×6 + 8×6)×2 = 376(dm^{2})$
答:剩下的部分的体积是$264dm^{3}$,剩下的部分的表面积是$376dm^{2}$。

思路分析
在这个长方体中截去一个最大的正方体,这个正方体的棱长对应长方体的高。(1)剩下部分的体积就等于长方体的体积减去棱长为 6 dm 的小正方体的体积,根据长方体的体积公式:$V = abh$,正方体的体积公式:$V = a^{3}$,把数据代入公式求出长方体与正方体的体积差即可。
(2)根据图形中的切割特点,剩下的部分的表面积比原来增加了边长为 6 dm 的 3 个正方形面的面积,同时减少了 3 个边长为 6 dm 的小正方形的面积,则剩下部分的表面积就等于原来长方体的表面积。
正确解答 $10×8×6 - 6×6×6 = 264(dm^{3})$
$(10×8 + 10×6 + 8×6)×2 = 376(dm^{2})$
答:剩下的部分的体积是$264dm^{3}$,剩下的部分的表面积是$376dm^{2}$。
答案:
解析:本题考查长方体和正方体体积与表面积的计算。
已知长方体的长为$10\mathrm{dm}$,宽为$8\mathrm{dm}$,高为$6\mathrm{dm}$,
根据长方体的体积公式$V = \text{长} × \text{宽} × \text{高}$,可得:
$V_{\text{长方体}} = 10 × 8 × 6 = 480(\mathrm{dm^3})$。
从这个长方体中截去一个最大的正方体,这个正方体的棱长对应长方体的高,即$6\mathrm{dm}$,
根据正方体的体积公式$V = \text{棱长}^3$,可得:
$V_{\text{正方体}} = 6 × 6 × 6 = 216(\mathrm{dm^3})$。
剩下部分的体积就等于长方体的体积减去正方体的体积,即:
$V_{\text{剩下}} = V_{\text{长方体}} - V_{\text{正方体}} = 480 - 216 = 264(\mathrm{dm^3})$。
根据长方体的表面积公式$S = 2 × (\text{长} × \text{宽} + \text{长} × \text{高} + \text{宽} × \text{高})$,可得:
$S_{\text{长方体}} = 2 × (10 × 8 + 10 × 6 + 8 × 6) = 2 × (80 + 60 + 48) = 2 × 188 = 376(\mathrm{dm^2})$。
由于截去正方体后,剩下部分的表面积比原来增加了边长为$6\mathrm{dm}$的$3$个正方形面的面积,同时减少了$3$个边长为$6\mathrm{dm}$的小正方形的面积,
所以剩下部分的表面积就等于原来长方体的表面积,即$376\mathrm{dm^2}$。
答:剩下的部分的体积是$264\mathrm{dm^3}$,剩下的部分的表面积是$376\mathrm{dm^2}$。
已知长方体的长为$10\mathrm{dm}$,宽为$8\mathrm{dm}$,高为$6\mathrm{dm}$,
根据长方体的体积公式$V = \text{长} × \text{宽} × \text{高}$,可得:
$V_{\text{长方体}} = 10 × 8 × 6 = 480(\mathrm{dm^3})$。
从这个长方体中截去一个最大的正方体,这个正方体的棱长对应长方体的高,即$6\mathrm{dm}$,
根据正方体的体积公式$V = \text{棱长}^3$,可得:
$V_{\text{正方体}} = 6 × 6 × 6 = 216(\mathrm{dm^3})$。
剩下部分的体积就等于长方体的体积减去正方体的体积,即:
$V_{\text{剩下}} = V_{\text{长方体}} - V_{\text{正方体}} = 480 - 216 = 264(\mathrm{dm^3})$。
根据长方体的表面积公式$S = 2 × (\text{长} × \text{宽} + \text{长} × \text{高} + \text{宽} × \text{高})$,可得:
$S_{\text{长方体}} = 2 × (10 × 8 + 10 × 6 + 8 × 6) = 2 × (80 + 60 + 48) = 2 × 188 = 376(\mathrm{dm^2})$。
由于截去正方体后,剩下部分的表面积比原来增加了边长为$6\mathrm{dm}$的$3$个正方形面的面积,同时减少了$3$个边长为$6\mathrm{dm}$的小正方形的面积,
所以剩下部分的表面积就等于原来长方体的表面积,即$376\mathrm{dm^2}$。
答:剩下的部分的体积是$264\mathrm{dm^3}$,剩下的部分的表面积是$376\mathrm{dm^2}$。
【典型例题】小明和小刚在家做测量不规则物体的体积实验。他们找了一个长方体容器,长 30 cm,宽 20 cm,高 10 cm。他们向容器里倒上一些水,水深达到了 6 cm。他们将一块石头完全浸没水中,结果水面上升后还溢出了 100 mL 水,这块石头的体积是多少立方厘米?
思路分析
缸里的水深 6 cm 而玻璃缸的高是 10 cm,则水面上升了$(10 - 6)cm$,石块的体积等于上升的水的体积加溢出水的体积,根据长方体的体积公式$V = abh$,即可列式解答。
正确解答 $30×20×(10 - 6) = 2400(cm^{3})$
$100mL = 100cm^{3}$
$2400 + 100 = 2500(cm^{3})$
答:这块石头的体积是$2500cm^{3}$。
思路分析
缸里的水深 6 cm 而玻璃缸的高是 10 cm,则水面上升了$(10 - 6)cm$,石块的体积等于上升的水的体积加溢出水的体积,根据长方体的体积公式$V = abh$,即可列式解答。
正确解答 $30×20×(10 - 6) = 2400(cm^{3})$
$100mL = 100cm^{3}$
$2400 + 100 = 2500(cm^{3})$
答:这块石头的体积是$2500cm^{3}$。
答案:
解析:
本题主要考查不规则物体的体积计算。
为了求解石头的体积,需要计算石头浸入水中后,水面上升的体积以及溢出的水的体积。
首先,计算水面上升的体积。
已知容器的长为30cm,宽为20cm,水面从6cm上升到10cm,所以水面上升了$10 - 6 = 4(cm)$。
根据长方体的体积公式,水面上升的体积为:
$V_{\text{上升}} = \text{长} × \text{宽} × \text{水面上升的高度}} = 30 × 20 × 4 = 2400 (cm^3)$。
接下来,计算溢出的水的体积。
题目已给出溢出的水的体积为100mL,根据$1mL = 1cm^3$,所以溢出的水的体积为$100cm^3$。
最后,石头的体积等于水面上升的体积加上溢出的水的体积,即:
$V_{\text{石头}} = V_{\text{上升}} + V_{\text{溢出}} = 2400 + 100 = 2500 (cm^3)$。
答案:
这块石头的体积是$2500cm^3$。
本题主要考查不规则物体的体积计算。
为了求解石头的体积,需要计算石头浸入水中后,水面上升的体积以及溢出的水的体积。
首先,计算水面上升的体积。
已知容器的长为30cm,宽为20cm,水面从6cm上升到10cm,所以水面上升了$10 - 6 = 4(cm)$。
根据长方体的体积公式,水面上升的体积为:
$V_{\text{上升}} = \text{长} × \text{宽} × \text{水面上升的高度}} = 30 × 20 × 4 = 2400 (cm^3)$。
接下来,计算溢出的水的体积。
题目已给出溢出的水的体积为100mL,根据$1mL = 1cm^3$,所以溢出的水的体积为$100cm^3$。
最后,石头的体积等于水面上升的体积加上溢出的水的体积,即:
$V_{\text{石头}} = V_{\text{上升}} + V_{\text{溢出}} = 2400 + 100 = 2500 (cm^3)$。
答案:
这块石头的体积是$2500cm^3$。
查看更多完整答案,请扫码查看


