2025年暑假衔接直通车五年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接直通车五年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
难点一 综合运用 添加或去掉几何体,保持某一个或几个方向看到的图形不变
【典型例题】在 中添一个
中添一个 (面与面相连),要使从右面看到的图形不变,有( )种不同的摆法,请在方格图中画出从右面看到的图形。
(面与面相连),要使从右面看到的图形不变,有( )种不同的摆法,请在方格图中画出从右面看到的图形。
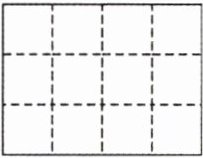
思路分析
这个立体图形由4个相同的小正方体组成,从右面能看到2个相同的正方形。在这个图形中添一个相同的小正方体,使从右面看到的图形不变,这个小正方体可添在前排的左边;后排右数第一个或第二个的前面;后排的左边和右边,即5种摆法。
正确解答 5
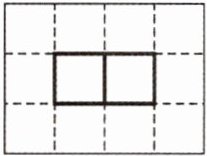
【典型例题】在
 中添一个
中添一个 (面与面相连),要使从右面看到的图形不变,有( )种不同的摆法,请在方格图中画出从右面看到的图形。
(面与面相连),要使从右面看到的图形不变,有( )种不同的摆法,请在方格图中画出从右面看到的图形。
思路分析
这个立体图形由4个相同的小正方体组成,从右面能看到2个相同的正方形。在这个图形中添一个相同的小正方体,使从右面看到的图形不变,这个小正方体可添在前排的左边;后排右数第一个或第二个的前面;后排的左边和右边,即5种摆法。
正确解答 5

答案:
解析:本题主要考查从不同方向观察立体图形。
要使从右面看到的图形不变,添加的小正方体可以在前排左边小正方体的前面或后面,也可以在后排从左往右数第一个小正方体的前面或第二个小正方体的前面,还可以在后排最左边小正方体的左边,共$5$种摆法。从右面看,能看到两列小正方形,左边一列$1$个,右边一列$1$个。
答案:5; 。
。
解析:本题主要考查从不同方向观察立体图形。
要使从右面看到的图形不变,添加的小正方体可以在前排左边小正方体的前面或后面,也可以在后排从左往右数第一个小正方体的前面或第二个小正方体的前面,还可以在后排最左边小正方体的左边,共$5$种摆法。从右面看,能看到两列小正方形,左边一列$1$个,右边一列$1$个。
答案:5;
 。
。 【典型例题】一个仓库里堆积着若干正方体货箱,这些箱子搬运比较困难,可是仓库管理员要清点一下箱子的数量,于是他将从正面、左面、上面看这堆货物,得到如下平面图形,你能根据这幅图帮助他清点箱子的数量吗?你是怎么清点的,请把你的想法写下来。
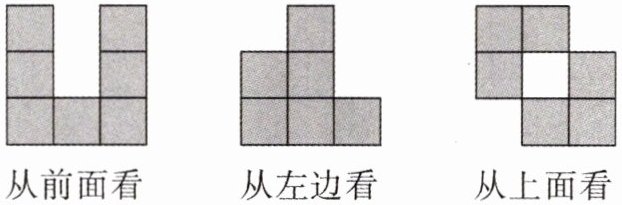
思路分析
根据从上面和从左面看到的图形可以知道第一排有1层,中间一排有3层,第三排有2层且中间那一排的中间没有货物;再根据从前面看到的图形知道中间那一排的左侧和右侧有3层,第三排的中间有1层,即 (图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量。
(图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量。
正确解答 $2 + 1 + 3 + 3 + 1 + 1 = 11$(个)
答:一共有11个箱子。

思路分析
根据从上面和从左面看到的图形可以知道第一排有1层,中间一排有3层,第三排有2层且中间那一排的中间没有货物;再根据从前面看到的图形知道中间那一排的左侧和右侧有3层,第三排的中间有1层,即
 (图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量。
(图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量。正确解答 $2 + 1 + 3 + 3 + 1 + 1 = 11$(个)
答:一共有11个箱子。
答案:
解析:本题考查根据三视图确定立体图形的形状以及计算其数量。通过从不同方向观察到的平面图形,分析出立体图形每层箱子的分布情况,进而计算出箱子的总数。
答案:
根据从上面和从左面看到的图形可知,第一排有$1$层,中间一排有$3$层,第三排有$2$层且中间那一排的中间没有货物;再根据从前面看到的图形可知,中间那一排的左侧和右侧有$3$层,第三排的中间有$1$层。
把从上面看到的图形上的数字相加即为箱子的总数量:$2 + 1 + 3 + 3 + 1 + 1 = 11$(个)
答:一共有$11$个箱子。
答案:
根据从上面和从左面看到的图形可知,第一排有$1$层,中间一排有$3$层,第三排有$2$层且中间那一排的中间没有货物;再根据从前面看到的图形可知,中间那一排的左侧和右侧有$3$层,第三排的中间有$1$层。
把从上面看到的图形上的数字相加即为箱子的总数量:$2 + 1 + 3 + 3 + 1 + 1 = 11$(个)
答:一共有$11$个箱子。
查看更多完整答案,请扫码查看


