《2025年暑假Happy假日八年级数学人教版》

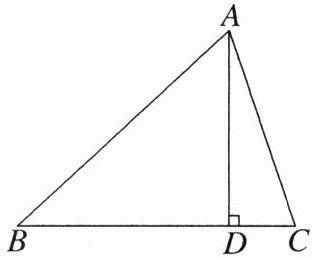
19. 若$△ABC$的底BC长为6 cm,高AD为x cm,
(1)写出$△ABC$的面积y与x之间的函数关系式;$y = 3x$
(2)指出关系式中的自变量与函数;自变量是$x$，函数是$y$
(3)当自变量$x=4cm$时,$△ABC$的面积为多少?$12cm^{2}$

答案： 【解析】：
（1）根据三角形面积公式$S = \frac{1}{2}\times底\times高$，已知底$BC = 6cm$，高$AD=xcm$，则$y=\frac{1}{2}\times6\times x$，化简可得$y = 3x$。
（2）在$y = 3x$这个关系式中，$x$的值可以自由变化，$y$的值随着$x$的变化而变化，所以自变量是$x$，函数是$y$。
（3）当$x = 4cm$时，把$x = 4$代入$y = 3x$中，可得$y=3\times4 = 12(cm^{2})$。
【答案】：
（1）$y = 3x$；
（2）自变量是$x$，函数是$y$；
（3）$12cm^{2}$。

20. 下表是佳佳往小姨家打长途电话的几次收费记录:
| 时间x/分 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 电话费y/元 | 0.6 | 1.2 | 1.8 | 2.4 | 3.0 | 3.6 | 4.2 |
回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是自变量的函数?
(2)帮助佳佳预测一下,如果她打电话用的时间是10分钟,那么需要付多少电话费?
(3)请你写出通话时间x(分)(x为正整数)与所要付的电话费y(元)之间的函数关系式.

答案： 【解析】：
(1)观察表格可知，表格中记录了通话时间$x$和电话费$y$的对应数据，所以反映的是通话时间$x$与电话费$y$这两个变量之间的关系。在这两个变量中，通话时间$x$的变化会引起电话费$y$的变化，所以自变量是通话时间$x$，电话费$y$随着通话时间$x$的变化而变化，所以电话费$y$是自变量$x$的函数。
(2)从表格中可以看出，通话时间每增加$1$分钟，电话费增加$0.6$元，说明电话费$y$与通话时间$x$成正比例关系。当$x = 1$时，$y = 0.6$，那么每分钟的费用是$0.6$元。所以当通话时间$x = 10$分钟时，电话费$y=0.6\times10 = 6$元。
(3)因为每分钟的电话费是$0.6$元，所以通话时间$x$（分）（$x$为正整数）与所要付的电话费$y$（元）之间的函数关系式为$y = 0.6x$（$x$为正整数）。
【答案】：
(1)反映了通话时间$x$与电话费$y$之间的关系；自变量是通话时间$x$；电话费$y$是自变量$x$的函数。
(2)$6$元。
(3)$y = 0.6x$（$x$为正整数）。