《2025年暑假Happy假日八年级数学人教版》

17. (8 分) 计算:
(1) $\frac{\sqrt{8}}{3 \sqrt{40}} \times \sqrt{5}$;
(2) $\sqrt{27} \times \sqrt{50} \div \sqrt{6}$;
(3) $\left(\frac{1}{2}\right)^{-1}-(\sqrt{3}-\sqrt{2})^{0}+|-3|$;
(4) $(\sqrt{3}+1)(\sqrt{3}-1)-\sqrt{(-3)^{2}}+\frac{1}{2-\sqrt{5}}$.

答案： 【解析】：
(1)
先将各项根式化简：$\sqrt{8} = 2\sqrt{2}$，$\sqrt{40}=2\sqrt{10}$。
则$\frac{\sqrt{8}}{3\sqrt{40}}\times\sqrt{5}=\frac{2\sqrt{2}}{3\times2\sqrt{10}}\times\sqrt{5}$。
对$\frac{2\sqrt{2}}{3\times2\sqrt{10}}$进行约分，$\frac{2\sqrt{2}}{3\times2\sqrt{10}}=\frac{\sqrt{2}}{3\sqrt{10}}$，再根据二次根式乘法法则$\frac{\sqrt{2}}{3\sqrt{10}}\times\sqrt{5}=\frac{\sqrt{2}\times\sqrt{5}}{3\sqrt{10}}$。
因为$\sqrt{2}\times\sqrt{5}=\sqrt{10}$，所以$\frac{\sqrt{2}\times\sqrt{5}}{3\sqrt{10}}=\frac{\sqrt{10}}{3\sqrt{10}}=\frac{1}{3}$。
(2)
先化简各项根式：$\sqrt{27}=3\sqrt{3}$，$\sqrt{50} = 5\sqrt{2}$。
则$\sqrt{27}\times\sqrt{50}\div\sqrt{6}=3\sqrt{3}\times5\sqrt{2}\div\sqrt{6}$。
根据二次根式乘法法则$3\sqrt{3}\times5\sqrt{2}=15\sqrt{6}$。
再根据二次根式除法法则$15\sqrt{6}\div\sqrt{6}=15$。
(3)
根据负整数指数幂的性质$a^{-p}=\frac{1}{a^{p}}(a\neq0)$，可得$(\frac{1}{2})^{-1}=\frac{1}{\frac{1}{2}} = 2$。
根据零指数幂的性质$a^{0}=1(a\neq0)$，可得$(\sqrt{3}-\sqrt{2})^{0}=1$。
根据绝对值的性质$\vert - 3\vert=3$。
所以$(\frac{1}{2})^{-1}-(\sqrt{3}-\sqrt{2})^{0}+\vert - 3\vert=2 - 1+3=4$。
(4)
根据平方差公式$(a + b)(a - b)=a^{2}-b^{2}$，则$(\sqrt{3}+1)(\sqrt{3}-1)=(\sqrt{3})^{2}-1^{2}=3 - 1=2$。
$\sqrt{(-3)^{2}}=\sqrt{9}=3$。
对$\frac{1}{2-\sqrt{5}}$进行分母有理化，分子分母同乘$2 + \sqrt{5}$，$\frac{1}{2-\sqrt{5}}=\frac{2+\sqrt{5}}{(2 - \sqrt{5})(2+\sqrt{5})}$，根据平方差公式$(2 - \sqrt{5})(2+\sqrt{5})=2^{2}-(\sqrt{5})^{2}=4 - 5=-1$，所以$\frac{2+\sqrt{5}}{(2 - \sqrt{5})(2+\sqrt{5})}=-(2+\sqrt{5})=-2-\sqrt{5}$。
则$(\sqrt{3}+1)(\sqrt{3}-1)-\sqrt{(-3)^{2}}+\frac{1}{2-\sqrt{5}}=2-3-2-\sqrt{5}=-3-\sqrt{5}$。
【答案】：
(1)$\frac{1}{3}$；
(2)$15$；
(3)$4$；
(4)$-3-\sqrt{5}$

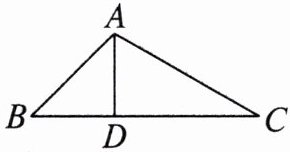
18. (6 分) 如图, 在 $\triangle A B C$ 中, $A D \perp B C, \angle B=45^{\circ}, \angle C=30^{\circ}, A D=1$, 求 $\triangle A B C$ 的周长.

$\sqrt{2}+\sqrt{3}+3$

答案： 【解析】：
- 因为$AD\perp BC$，所以$\angle ADB = \angle ADC = 90^{\circ}$。
- 在$Rt\triangle ABD$中，$\angle B = 45^{\circ}$，$\angle ADB = 90^{\circ}$，所以$\angle BAD = 180^{\circ}-\angle B - \angle ADB = 45^{\circ}$，则$\angle B=\angle BAD$，所以$BD = AD = 1$。
根据勾股定理$AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{1^{2}+1^{2}}=\sqrt{2}$。
- 在$Rt\triangle ADC$中，$\angle C = 30^{\circ}$，$\angle ADC = 90^{\circ}$，所以$AC = 2AD = 2$。
根据勾股定理$DC=\sqrt{AC^{2}-AD^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。
- 所以$BC = BD + DC = 1+\sqrt{3}$。
- 则$\triangle ABC$的周长为$AB + BC + AC=\sqrt{2}+1+\sqrt{3}+2=\sqrt{2}+\sqrt{3}+3$。
【答案】：$\sqrt{2}+\sqrt{3}+3$