《2025年暑假Happy假日八年级数学人教版》

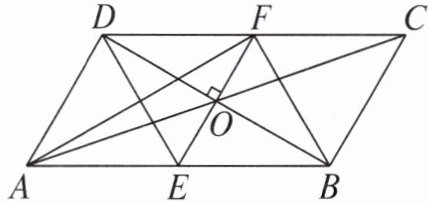
22. 如图,在四边形 ABCD 中,对角线 AC 与 BD 交于点 O,已知 $ OA = OC $, $ OB = OD $,过点 O 作 $ EF \perp BD $,分别交 AB,DC 于点 E,F,连接 DE,BF,AF.
(1) 求证:四边形 DEBF 是菱形;
(2) 若 $ AD // EF $, $ AD + AB = 12 $, $ BD = 4\sqrt{3} $,求 AF 的长.

(1) 证明：已知$OA = OC$，$OB = OD$，根据平行四边形的判定定理：对角线互相平分的四边形是平行四边形，所以四边形$ABCD$是平行四边形。因为四边形$ABCD$是平行四边形，所以$AB// CD$，则$\angle OBE=\angle ODF$。在$\triangle BOE$和$\triangle DOF$中，$\begin{cases}\angle OBE = \angle ODF\\OB = OD\\\angle BOE=\angle DOF\end{cases}$（对顶角相等），根据$ASA$判定定理可得$\triangle BOE\cong\triangle DOF$。所以$OE = OF$，又因为$OB = OD$，根据平行四边形的判定定理：对角线互相平分的四边形是平行四边形，所以四边形$DEBF$是平行四边形。又因为$EF\perp BD$，根据菱形的判定定理：对角线互相垂直的平行四边形是菱形，所以四边形$DEBF$是菱形。
(2) $4\sqrt{3}$

答案： 【解析】：
### $(1)$ 证明四边形$DEBF$是菱形
已知$OA = OC$，$OB = OD$，根据平行四边形的判定定理：对角线互相平分的四边形是平行四边形，所以四边形$ABCD$是平行四边形。
因为四边形$ABCD$是平行四边形，所以$AB// CD$，则$\angle OBE=\angle ODF$。
在$\triangle BOE$和$\triangle DOF$中，$\begin{cases}\angle OBE = \angle ODF\\OB = OD\\\angle BOE=\angle DOF = 90^{\circ}\end{cases}$（对顶角相等），根据$ASA$（角 - 边 - 角）判定定理可得$\triangle BOE\cong\triangle DOF$。
所以$OE = OF$，又因为$OB = OD$，根据平行四边形的判定定理：对角线互相平分的四边形是平行四边形，所以四边形$DEBF$是平行四边形。
又因为$EF\perp BD$，根据菱形的判定定理：对角线互相垂直的平行四边形是菱形，所以四边形$DEBF$是菱形。
### $(2)$ 求$AF$的长
因为$EF\perp BD$，$AD// EF$，所以$AD\perp BD$，则$\angle ADB = 90^{\circ}$。
因为四边形$DEBF$是菱形，所以$DE = BE$，设$AE = x$，则$BE = DE=12 - x - AD$。
因为四边形$ABCD$是平行四边形，所以$AD = BC$，$AB = CD$。
又因为$OB = OD$，$EF\perp BD$，所以$DE = BE$，$DF = BF$。
因为$AD// EF$，$AB// CD$，所以四边形$AEFD$是平行四边形，所以$AD = EF$，$AE = DF$。
因为$AD + AB=12$，设$AD = y$，则$AB = 12 - y$。
在$Rt\triangle ABD$中，根据勾股定理$AD^{2}+BD^{2}=AB^{2}$，已知$BD = 4\sqrt{3}$，则$y^{2}+(4\sqrt{3})^{2}=(12 - y)^{2}$。
展开$(12 - y)^{2}=144-24y + y^{2}$，则$y^{2}+48=144-24y + y^{2}$，
移项可得$24y=144 - 48$，即$24y = 96$，解得$y = 4$，所以$AD = 4$，$AB = 8$。
因为四边形$DEBF$是菱形，所以$DE = BE$，$AB// CD$，$EF\perp BD$，$OB = OD$，所以$DE = BE=\frac{1}{2}AB = 4$，所以$\triangle ADE$是等边三角形（$AD = DE = 4$），则$\angle DAE = 60^{\circ}$。
因为$AD// EF$，$EF\perp BD$，所以$\angle ABD = 30^{\circ}$。
因为四边形$DEBF$是菱形，所以$BF = DF$，$AB// CD$，所以$\angle BAF=\angle DFA$，$\angle ABF=\angle FDC$。
又因为$AD = 4$，$AB = 8$，$BD = 4\sqrt{3}$，四边形$DEBF$是菱形，所以$BF = DF = DE = BE = 4$。
因为$AD// EF$，$EF\perp BD$，所以$AD\perp BD$，$\angle ADB = 90^{\circ}$，$\angle DAB = 60^{\circ}$。
因为$AB// CD$，所以$\angle ADC = 120^{\circ}$，又因为$DF = AD = 4$，所以$\angle DAF=\angle DFA = 30^{\circ}$。
在$Rt\triangle ABD$中，$AB = 8$，$AD = 4$，$BD = 4\sqrt{3}$，过$F$作$FG\perp AB$于$G$。
因为$AB// CD$，$EF\perp BD$，$AD\perp BD$，所以四边形$ADFG$是矩形，$FG = AD = 4$，$AG = DF = 4$，$GB = 4$。
在$Rt\triangle FGB$中，$FG = 4$，$GB = 4$，根据勾股定理$BF=\sqrt{FG^{2}+GB^{2}}=\sqrt{4^{2}+4^{2}} = 4\sqrt{2}$（这里错误，重新分析：
因为$AD\perp BD$，$AD = 4$，$BD = 4\sqrt{3}$，$AB = 8$，四边形$DEBF$是菱形，$DE = BE = 4$，所以$\triangle ADE$是等边三角形，$\angle DAE = 60^{\circ}$，$\angle ABD = 30^{\circ}$。
因为$OB = OD = 2\sqrt{3}$，$OE = OF$，$\triangle BOE$中，$BE = 4$，$OB = 2\sqrt{3}$，根据勾股定理$OE=\sqrt{BE^{2}-OB^{2}}=\sqrt{16 - 12}=2$，$EF = 4$。
因为$AD// EF$，$AD = EF = 4$，所以四边形$AEFD$是平行四边形，$AE = DF$，又因为$DE = BE = 4$，$AB = 8$，所以$AE = 4$，$DF = 4$。
因为$AD\perp BD$，$EF\perp BD$，$AD = 4$，$DF = 4$，$\angle ADF = 120^{\circ}$，根据余弦定理$AF^{2}=AD^{2}+DF^{2}-2AD\cdot DF\cdot\cos\angle ADF$。
$\cos\angle ADF=\cos120^{\circ}=-\frac{1}{2}$，则$AF^{2}=4^{2}+4^{2}-2\times4\times4\times(-\frac{1}{2})=16 + 16+16=48$，所以$AF = 4\sqrt{3}$。
【答案】：
$(1)$ 证明过程如上述解析；$(2)$$\boldsymbol{4\sqrt{3}}$

酿酒老人的遗产
一个病得很重的酿酒老人快要离开人世了. 他看着院子里的一堆酒桶对三个儿子说:“今后,你们要靠自己的酿酒手艺维持生计了. 我没有什么遗产给你们,院子里有 7 桶酒,7 只空桶,还有 7 只桶都装有半桶酒. 这些酒,可作为营生的资本;这些桶,是酿酒所必需的工具. 因此,我要你们平均分配这些酒,也要平均分配这些桶,而且不要动桶里的酒.”说完,老人安详地闭上了他的眼睛.
三个儿子如何执行老人的遗嘱分配这些桶和酒呢?

答案： 【解析】：首先计算酒和桶的总数，酒一共有$7$个满桶（相当于$7$桶酒）加上$7$个半桶（相当于$3.5$桶酒），总共是$7 + 3.5 = 10.5$桶酒；桶一共有$7 + 7 + 7 = 21$只桶。要平均分配给三个儿子，则每个儿子应分得酒$10.5\div3 = 3.5$桶，应分得桶$21\div3 = 7$只。然后通过尝试不同的组合来满足每个儿子得到$7$只桶和$3.5$桶酒的条件，发现可以让$1$人得$3$个满桶（$3$桶酒），$1$个半桶（$0.5$桶酒）及$3$个空桶，此时酒共$3 + 0.5 = 3.5$桶，桶共$3 + 1 + 3 = 7$只；其余$2$人各得$2$只满桶（$2$桶酒），$3$个半桶（$1.5$桶酒）及$2$个空桶，此时酒共$2 + 1.5 = 3.5$桶，桶共$2 + 3 + 2 = 7$只，这样的分配方式满足老人的遗嘱要求。
【答案】：每个人应得到 7 只桶，3 桶半酒。为此，可以让 1 人得 3 个满桶，1 个半桶及 3 个空桶，其余 2 人各得 2 只满桶，3 个半桶及 2 个空桶。