《2025年暑假Happy假日七年级理科五四制》

21. (8分)已知$5a+2$的立方根是3,$3a+b-1$的算术平方根是4,$c$是$\sqrt {13}$的整数部分.
(1)求$a,b,c$的值;
(2)求$3a-b+c$的平方根.

答案：
(1)$a = 5$，$b = 2$，$c = 3$；
(2)$\pm4$

22. (6分)如图,已知$DE⊥AC,∠AGF=∠ABC,∠1+∠2=180^{\circ }$,试判断$BF$与$AC$的位置关系,并说明理由.

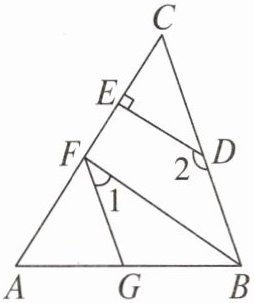
$BF$与$AC$的位置关系是$BF\perp AC$.

答案： $BF\perp AC$

23. (6分)小嘉准备解答题目:解二元一次方程组$\left\{\begin{array}{l} 2x-3y=13,\\ □x+4y=-6,\end{array}\right. $发现系数“□”印刷不清楚.
(1)他把“□”猜成3,请你解二元一次方程组$\left\{\begin{array}{l} 2x-3y=13,\\ 3x+4y=-6;\end{array}\right. $
解：方程组的解为$\boldsymbol{\begin{cases}x=2 \\y=-3 \\\end{cases}}$。
(2)妈妈说:“你猜错了,我看到该题标准答案$x$与$y$是一对相反数.”通过计算说明原题中的“□”是几.
解：原题中的“□”是-2。

答案： $(1)$解方程组$\begin{cases}2x - 3y = 13 \\3x + 4y = -6 \\\end{cases}$
解：
给方程$2x - 3y = 13$两边同时乘以$4$，方程$3x + 4y = -6$两边同时乘以$3$，得到新的方程组：
$\begin{cases}8x - 12y = 52&(a)\\9x + 12y = -18&(b)\\\end{cases}$
将$(a)$式与$(b)$式相加消去$y$：
$\begin{aligned}(8x - 12y)+(9x + 12y)&=52+( - 18)\\8x - 12y + 9x + 12y&=52 - 18\\17x&=34\\x&=2\end{aligned}$
把$x = 2$代入$2x - 3y = 13$得：
$2\times2 - 3y = 13$，即$4 - 3y = 13$，
移项可得$-3y = 13 - 4$，即$-3y = 9$，
解得$y = - 3$。
所以方程组$\begin{cases}2x - 3y = 13 \\3x + 4y = -6 \\\end{cases}$的解为$\begin{cases}x = 2 \\y = - 3 \\\end{cases}$。
$(2)$求原题中“$□$”的值
解：
因为$x$与$y$是一对相反数，所以$y=-x$。
将$y = - x$代入$2x - 3y = 13$得：
$2x - 3\times(-x)=13$，
即$2x + 3x = 13$，
$5x = 13$，
解得$x=\frac{13}{5}$，则$y =-\frac{13}{5}$。
把$x=\frac{13}{5}$，$y =-\frac{13}{5}$代入$□x + 4y = - 6$得：
$\frac{13}{5}\times□+4\times(-\frac{13}{5})=-6$，
$\frac{13}{5}\times□-\frac{52}{5}=-6$，
方程两边同时乘以$5$得：$13\times□-52=-30$，
移项可得$13\times□=-30 + 52$，
即$13\times□=22$，
解得$□ = - 2$。
综上，$(1)$方程组的解为$\boldsymbol{\begin{cases}x = 2 \\y = - 3 \\\end{cases}}$；$(2)$原题中的“$□$”是$\boldsymbol{-2}$。