《2025年暑假Happy假日七年级数学人教版》

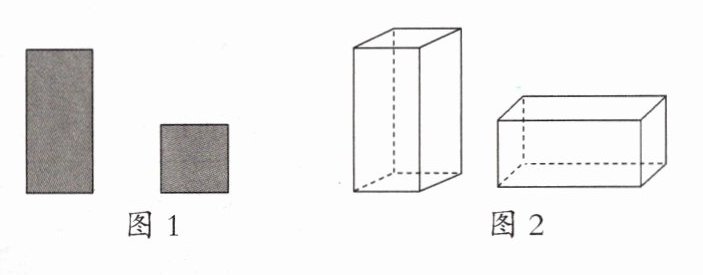
16. 用如图 1 中的长方形和正方形纸板作侧面和底面,做成如图 2 的竖式和横式两种无盖纸盒.现在仓库里有 1000 张正方形纸板和 2000 张长方形纸板,问两种纸盒各做多少个,恰好将库存纸板用完?

做竖式纸盒200个，横式纸盒400个，恰好将库存纸板用完。

答案： 【解析】：
设做竖式纸盒$x$个，横式纸盒$y$个。
- 对于正方形纸板：
竖式纸盒底面是$1$个正方形，横式纸盒底面是$2$个正方形，已知共有$1000$张正方形纸板，则$x + 2y=1000$。
- 对于长方形纸板：
竖式纸盒侧面是$4$个长方形，横式纸盒侧面是$3$个长方形，已知共有$2000$张长方形纸板，则$4x + 3y=2000$。
联立方程组$\begin{cases}x + 2y=1000\\4x + 3y=2000\end{cases}$
由$x + 2y=1000$可得$x = 1000 - 2y$，将其代入$4x + 3y=2000$中：
$\begin{aligned}4(1000 - 2y)+3y&=2000\\4000-8y + 3y&=2000\\- 5y&=2000 - 4000\\-5y&=-2000\\y&=400\end{aligned}$
把$y = 400$代入$x = 1000 - 2y$，得$x=1000-2\times400 = 200$。
【答案】：
做竖式纸盒$200$个，横式纸盒$400$个，恰好将库存纸板用完。

17. 一家商店进行装修,若请甲、乙两个装修队同时施工,8 天可以完成,需付两队费用共 3520 元,若先请甲队单独做 6 天,再请乙队单独做 12 天可以完成,需付费用共 3480 元,问:
(1)甲、乙两队工作一天,商店各应付多少钱?
(2)已知甲队单独完成需 12 天,乙队单独完成需 24 天,单独请哪个队,商店所需费用最少?
(3)若装修完后,商店每天可赢利 200 元,你认为如何安排施工更有利于商店?请你帮助商店做决策.[可用(1)(2)问的条件及结论]

答案： 【解析】：
(1)设甲队工作一天商店应付$x$元，乙队工作一天商店应付$y$元。
根据“若请甲、乙两个装修队同时施工，$8$天可以完成，需付两队费用共$3520$元”，可列方程$8x + 8y = 3520$；
根据“若先请甲队单独做$6$天，再请乙队单独做$12$天可以完成，需付费用共$3480$元”，可列方程$6x + 12y = 3480$。
则可得方程组$\begin{cases}8x + 8y = 3520\\6x + 12y = 3480\end{cases}$
对第一个方程进行化简：$8x + 8y = 3520$两边同时除以$8$得$x + y = 440$，即$x = 440 - y$。
将$x = 440 - y$代入$6x + 12y = 3480$中，得到$6(440 - y)+12y = 3480$。
去括号得$2640-6y + 12y = 3480$。
移项合并得$6y = 3480 - 2640$，即$6y = 840$，解得$y = 140$。
把$y = 140$代入$x = 440 - y$，得$x = 440 - 140 = 300$。
所以甲队工作一天商店应付$300$元，乙队工作一天商店应付$140$元。
(2)已知甲队单独完成需$12$天，乙队单独完成需$24$天。
甲队单独完成所需费用为：$12\times300 = 3600$（元）
乙队单独完成所需费用为：$24\times140 = 3360$（元）
因为$3360\lt3600$，所以单独请乙队，商店所需费用最少。
(3)
①若单独请甲队施工，需$12$天完成，商店需付费用$3600$元，这$12$天商店少盈利$200\times12 = 2400$元，那么相当于花费$3600 + 2400 = 6000$元。
②若单独请乙队施工，需$24$天完成，商店需付费用$3360$元，这$24$天商店少盈利$200\times24 = 4800$元，那么相当于花费$3360+4800 = 8160$元。
③若请甲、乙两队同时施工，需$8$天完成，商店需付费用$3520$元，这$8$天商店少盈利$200\times8 = 1600$元，那么相当于花费$3520 + 1600 = 5120$元。
因为$5120\lt6000\lt8160$，所以请甲、乙两队同时施工更有利于商店。
【答案】：
(1)甲队$300$元，乙队$140$元；
(2)乙队；
(3)请甲、乙两队同时施工更有利于商店。