《2025年暑假Happy假日七年级数学人教版》

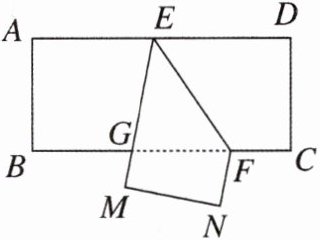
17. 如图，把一张长方形纸片$ABCD$沿$EF$折叠，若$∠EFG=50^{\circ }$，求$∠DEG$的度数。

$100^{\circ}$

答案： 【解析】：
- 因为四边形$ABCD$是长方形，所以$AD// BC$。
- 根据两直线平行，内错角相等，可得$\angle DEF=\angle EFG = 50^{\circ}$。
- 又因为长方形纸片$ABCD$沿$EF$折叠，所以$\angle GEF=\angle DEF = 50^{\circ}$。
- 那么$\angle DEG=\angle DEF+\angle GEF = 50^{\circ}+50^{\circ}=100^{\circ}$。
【答案】：$100^{\circ}$

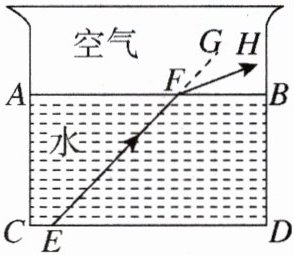
18. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射。如图，水面$AB$与水杯下沿$CD$平行，光线$EF$从水中射向空气时发生折射，光线变成$FH$，点$G$在射线$EF$上，已知$∠HFB=20^{\circ }$，$∠FED=45^{\circ }$，求$∠GFH$的度数。

$25^{\circ}$

答案： 【解析】：
因为$AB// CD$，根据“两直线平行，内错角相等”，所以$\angle GFB = \angle FED = 45^{\circ}$。
又因为$\angle HFB = 20^{\circ}$，所以$\angle GFH=\angle GFB - \angle HFB$。
将$\angle GFB = 45^{\circ}$，$\angle HFB = 20^{\circ}$代入可得：$\angle GFH = 45^{\circ}-20^{\circ}=25^{\circ}$。
【答案】：$25^{\circ}$