第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
17. 作图题.
(1)3月12日是植树节,图①中“树”需进行平移,请将“树根”A移到点F处,作出平移后的“树”;
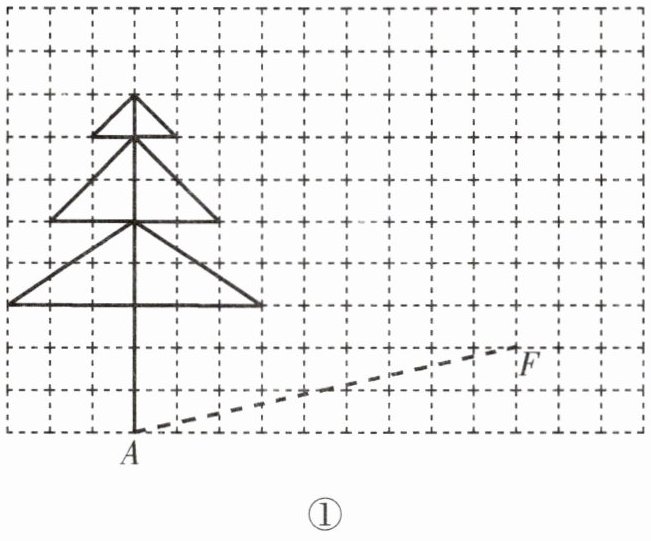
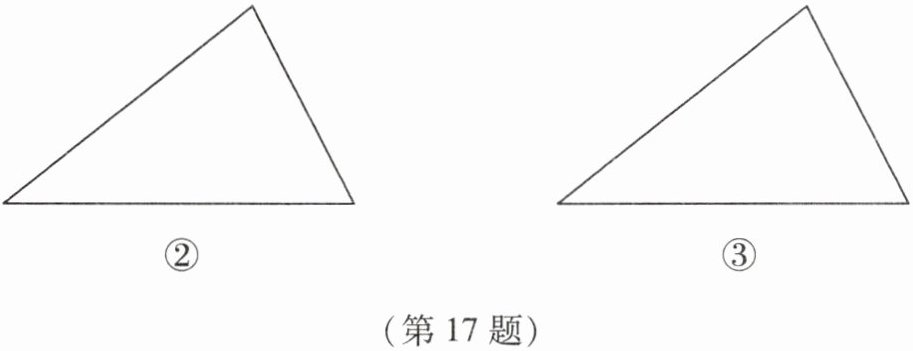
(2)小明家有一块三角形菜地,要种面积相等的四种蔬菜,请你设计两种方案,把这块地分成四块面积相等的三角形地块分别种植这四种蔬菜.
(1)3月12日是植树节,图①中“树”需进行平移,请将“树根”A移到点F处,作出平移后的“树”;

(2)小明家有一块三角形菜地,要种面积相等的四种蔬菜,请你设计两种方案,把这块地分成四块面积相等的三角形地块分别种植这四种蔬菜.

答案:
$(1)$ 平移作图
平移的性质:平移不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
- 步骤一:连接$AF$。
- 步骤二:分别过“树”的其他关键点作与$AF$平行且相等的线段,确定这些关键点平移后的对应点。
步骤三:按照原“树”的形状,顺次连接平移后的对应点,得到平移后的“树”。
$(2)$ 三角形面积相等的分割方案
三角形面积公式为$S = \frac{1}{2}ah$($a$为底,$h$为高)。
方案一**:
把三角形的一条边四等分,然后分别连接顶点与这些等分点。
理由:因为这四个小三角形等底(把底边四等分,所以底相等)同高(高是从顶点到底边的距离,都相等),根据三角形面积公式$S=\frac{1}{2}ah$,所以它们的面积相等。
方案二**:
先取三角形三边的中点,然后连接三边中点。
理由:根据三角形中位线定理,中位线平行于第三边且等于第三边的一半。可以证明这四个小三角形全等(三边分别相等的三角形全等),全等三角形面积相等。
综上,$(1)$ 按照平移性质作出平移后的“树”(具体图形根据上述步骤绘制);$(2)$ 方案一:把三角形一边四等分,连接顶点与等分点;方案二:连接三角形三边中点 。
平移的性质:平移不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
- 步骤一:连接$AF$。
- 步骤二:分别过“树”的其他关键点作与$AF$平行且相等的线段,确定这些关键点平移后的对应点。
步骤三:按照原“树”的形状,顺次连接平移后的对应点,得到平移后的“树”。
$(2)$ 三角形面积相等的分割方案
三角形面积公式为$S = \frac{1}{2}ah$($a$为底,$h$为高)。
方案一**:
把三角形的一条边四等分,然后分别连接顶点与这些等分点。
理由:因为这四个小三角形等底(把底边四等分,所以底相等)同高(高是从顶点到底边的距离,都相等),根据三角形面积公式$S=\frac{1}{2}ah$,所以它们的面积相等。
方案二**:
先取三角形三边的中点,然后连接三边中点。
理由:根据三角形中位线定理,中位线平行于第三边且等于第三边的一半。可以证明这四个小三角形全等(三边分别相等的三角形全等),全等三角形面积相等。
综上,$(1)$ 按照平移性质作出平移后的“树”(具体图形根据上述步骤绘制);$(2)$ 方案一:把三角形一边四等分,连接顶点与等分点;方案二:连接三角形三边中点 。
18. 如图,在正方形ABCD中,E是BC上一点,连结AE. 请添加一条线段,使所得图形是一个轴对称图形. (要求:画出示意图,并作出对称轴)


答案:
1. 首先,我们可以考虑添加$DE$:
因为正方形$ABCD$中,$AB = DC$,$\angle B=\angle C = 90^{\circ}$,$BE$和$CE$的关系不确定,若添加$DE$,根据正方形的对称性,对称轴为正方形$ABCD$的对称轴(如过$AD$中点和$BC$中点的直线$l_1$,或对角线$AC$、$BD$所在直线,这里以过$AD$中点和$BC$中点的直线为例)。
示意图:连接$DE$,过$AD$中点$M$和$BC$中点$N$作直线$l_1$,$\triangle ABE$与$\triangle DCE$关于直线$l_1$对称(因为$AB = DC$,$BM=CN$,$\angle B=\angle C$,根据全等三角形$SAS$判定,$\triangle ABE\cong\triangle DCE$,且直线$l_1$垂直平分$AD$和$BC$,所以图形关于直线$l_1$对称)。
2. 其次,我们可以考虑添加$AE$的垂直平分线与$CD$的交点$F$,连接$AF$:
设$AE$的垂直平分线为$l_2$,因为$AB = AD$,$\angle B=\angle D = 90^{\circ}$,若$BE = DF$(由垂直平分线性质和正方形性质可推得),根据$SAS$($AB = AD$,$\angle B=\angle D$,$BE = DF$),$\triangle ABE\cong\triangle ADF$。
对称轴为$AE$的垂直平分线$l_2$。
(答案不唯一,以上是两种常见的添加方法及对称轴的确定)
因为正方形$ABCD$中,$AB = DC$,$\angle B=\angle C = 90^{\circ}$,$BE$和$CE$的关系不确定,若添加$DE$,根据正方形的对称性,对称轴为正方形$ABCD$的对称轴(如过$AD$中点和$BC$中点的直线$l_1$,或对角线$AC$、$BD$所在直线,这里以过$AD$中点和$BC$中点的直线为例)。
示意图:连接$DE$,过$AD$中点$M$和$BC$中点$N$作直线$l_1$,$\triangle ABE$与$\triangle DCE$关于直线$l_1$对称(因为$AB = DC$,$BM=CN$,$\angle B=\angle C$,根据全等三角形$SAS$判定,$\triangle ABE\cong\triangle DCE$,且直线$l_1$垂直平分$AD$和$BC$,所以图形关于直线$l_1$对称)。
2. 其次,我们可以考虑添加$AE$的垂直平分线与$CD$的交点$F$,连接$AF$:
设$AE$的垂直平分线为$l_2$,因为$AB = AD$,$\angle B=\angle D = 90^{\circ}$,若$BE = DF$(由垂直平分线性质和正方形性质可推得),根据$SAS$($AB = AD$,$\angle B=\angle D$,$BE = DF$),$\triangle ABE\cong\triangle ADF$。
对称轴为$AE$的垂直平分线$l_2$。
(答案不唯一,以上是两种常见的添加方法及对称轴的确定)
查看更多完整答案,请扫码查看


