《2025年假日数学吉林出版集团股份有限公司七年级数学华师大版》

6. 给出下列正多边形：①正三角形；②正方形；③正六边形；④正八边形. 用上述正多边形中的一种能够铺满地面的是____. (填序号)

答案： 6. ①②③

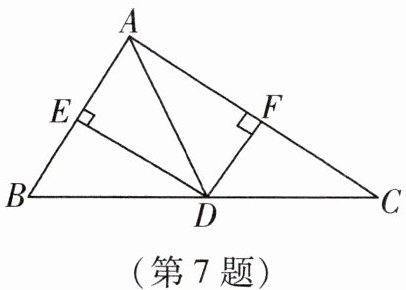
7. 如图,在 $ \triangle ABC $ 中, $ AD $ 为中线, $ DE $ 和 $ DF $ 分别为 $ \triangle ADB $ 和 $ \triangle ADC $ 的高,若 $ AB = 6 $, $ AC = 8 $, $ DF = 3 $,则 $ DE = $____.

答案： 7. 4

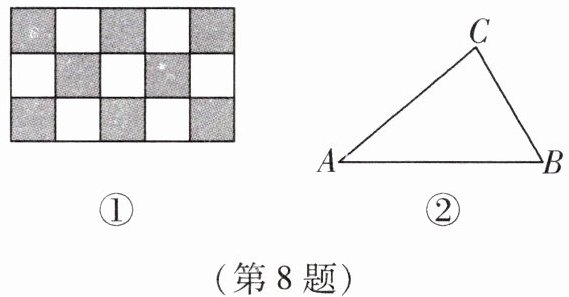
8. 如图①,用地砖铺地,要求砖与砖严丝合缝,不留空隙,把地面全部覆盖. 从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖. 任意剪出一些形状、大小相同的三角形纸板(如图②),它们能铺满平面,依据是____.

答案： 8. 三角形的内角和为$180^{\circ}$

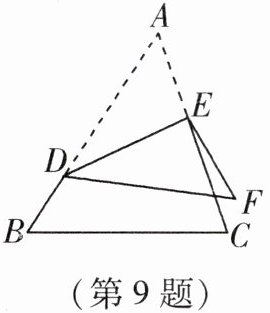
9. 如图,将 $ \triangle ABC $ 沿 $ DE $ 折叠,使点 $ A $ 落在点 $ F $ 处.
嘉嘉认为此题 $ \angle A $ 与 $ \angle BDF $、 $ \angle CEF $ 的关系为： $ \angle BDF + \angle CEF = 2 \angle A $；
淇淇认为此题 $ \angle A $ 与 $ \angle BDF $、 $ \angle CEF $ 的关系为： $ \angle BDF + \angle CEF = \angle A $.
老师说她俩的答案都有错误,同学们,你们认为 $ \angle A $ 与 $ \angle BDF $、 $ \angle CEF $ 的关系是____.

答案： 9. $∠BDF - ∠CEF = 2∠A$

10. 在 $ \triangle ABC $ 中, $ \angle ABC $、 $ \angle ACB $ 的平分线交于点 $ O $,与 $ \angle ACB $ 相邻的外角的平分线所在直线与 $ \angle ABC $ 的平分线相交于点 $ D $,和与 $ \angle ABC $ 相邻的外角的平分线相交于点 $ E $,则下列结论一定正确的是____. (填序号)

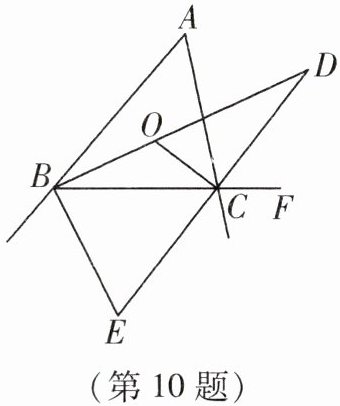
① $ \angle BOC = 90^{\circ} + \frac{1}{2} \angle A $；② $ \angle D = \frac{1}{2} \angle A $；③ $ \angle E = \angle A $；④ $ \angle E + \angle DCF = 90^{\circ} + \angle ABD $.

答案： 10. ①②④