《2025年假日数学吉林出版集团股份有限公司七年级数学华师大版》

17. 如图,在四边形ABCD中,设$\angle A= \alpha$,$\angle D= \beta$,$\angle P$为四边形ABCD的内角$\angle ABC与外角\angle DCE$的平分线所在直线相交而形成的锐角.

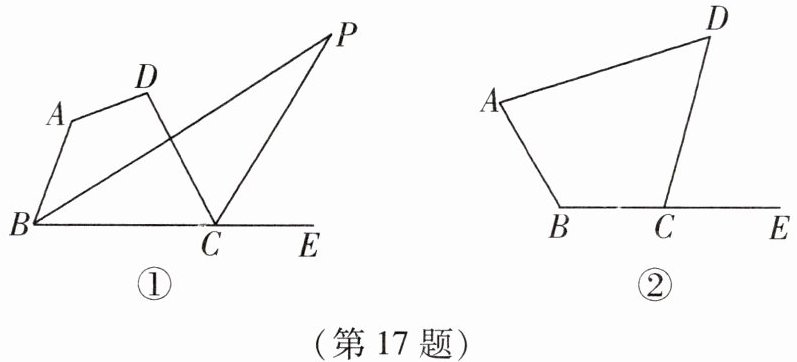
(1)如图①,若$\alpha+\beta＞180^{\circ}$,求$\angle P$的度数；(用含$\alpha$、$\beta$的代数式表示)
(2)如图②,若$\alpha+\beta＜180^{\circ}$,请在图②中画出$\angle P$,并求得$\angle P = $______.(用含$\alpha$、$\beta$的代数式表示)

答案： 17. 解：
(1)$\because \angle ABC + \angle DCB = 360^{\circ} - (\alpha + \beta)$，
$\therefore \angle ABC + (180^{\circ} - \angle DCE) = 360^{\circ} - (\alpha + \beta) = 2\angle PBC + (180^{\circ} - 2\angle DCP) = 180^{\circ} - 2(\angle DCP - \angle PBC) = 180^{\circ} - 2\angle P$，
$\therefore 360^{\circ} - (\alpha + \beta) = 180^{\circ} - 2\angle P$，
$2\angle P = \alpha + \beta - 180^{\circ}$，
$\therefore \angle P = \frac{1}{2}(\alpha + \beta) - 90^{\circ}$.
(2)$90^{\circ} - \frac{1}{2}(\alpha + \beta)$