《2025年假日数学吉林出版集团股份有限公司七年级数学华师大版》

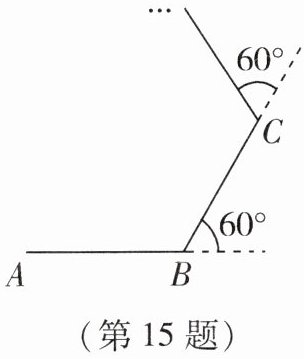
15. 如图,小东在操场的中心位置,从点A出发,每走6m向左转$60^{\circ}$.
(1)小东能否走回点A？若能回到点A,则需走多少米,走过的路径是一个什么图形？请说明理由；(路径为点$A \to点B \to点C ……\to $)
(2)求这个图形的内角和.

答案： 15.
(1)能，小东一共走了 36 m. 正六边形
(2)$720^{\circ}$

16.(1)填表：
| $n$(凸多边形的边数) | 3 | 4 | 5 | …$$ |
| $m$(凸多边形中角度等于$135^{\circ}$的内角个数的最大值) | | | | …$$ |
(2)猜想给定一个正整数n,凸n边形最多有m个内角等于$135^{\circ}$,则m与n之间有怎样的关系？
(3)取$n = 7$验证你的猜想是否成立？如果不成立,请给出凸n边形中最多有多少个内角等于$135^{\circ}$,并说明理由.

答案： 16.
(1)1 2 3
(2)$m = n - 2$
(3)当$3 \leq n \leq 5$时，凸$n$边形最多有$n - 2$个内角等于$135^{\circ}$；当$6 \leq n \leq 7$时，凸$n$边形最多有$n - 1$个内角等于$135^{\circ}$；当$n = 8$时，凸$n$边形最多有 8 个内角等于$135^{\circ}$；当$n ＞ 8$时，凸$n$边形最多有 7 个内角等于$135^{\circ}$.