第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
10. 小亮爸爸行驶在最高限速$80km/h$的路段上,某时刻的导航界面如图所示,前方第一个路口显示绿灯倒计时$32s$,第二个路口显示红灯倒计时$44s$,此时车辆分别距两个路口$480m和880m$. 已知第一个路口红、绿灯设定时间分别是$30s$、$50s$,第二个路口红、绿灯设定时间分别是$45s$、$60s$. 若不考虑其他因素,小亮爸爸以不低于$40km/h$的车速全程匀速行驶且不遇到红灯通过这两个路口(在红、绿灯切换瞬间不可通过),则车速$v$(单位:$km/h$)的取值范围是____.


答案:
$54 < v < 72$
11. 解不等式组$\left\{\begin{array}{l} 3x + 3 \geq 2x,①\\ 1 - 2x \geq -7.②\end{array} \right. $
请结合题意填空,完成本题的解答.
(1)解不等式①,得____;
(2)解不等式②,得____;
(3)把不等式①和②的解集在数轴上表示出来;

(4)原不等式组的解集为____.
请结合题意填空,完成本题的解答.
(1)解不等式①,得____;
(2)解不等式②,得____;
(3)把不等式①和②的解集在数轴上表示出来;

(4)原不等式组的解集为____.
答案:
1. 解不等式①:
解$3x + 3\geq2x$,移项可得$3x-2x\geq - 3$,即$x\geq - 3$。
2. 解不等式②:
解$1 - 2x\geq - 7$,移项得$-2x\geq - 7 - 1$,即$-2x\geq - 8$,两边同时除以$-2$,不等号方向改变,得$x\leq4$。
3.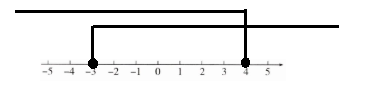
4. 原不等式组的解集:
取$x\geq - 3$与$x\leq4$的公共部分,所以原不等式组的解集为$-3\leq x\leq4$。
故答案依次为:
(1)$x\geq - 3$;
(2)$x\leq4$;
(4)$-3\leq x\leq4$。
1. 解不等式①:
解$3x + 3\geq2x$,移项可得$3x-2x\geq - 3$,即$x\geq - 3$。
2. 解不等式②:
解$1 - 2x\geq - 7$,移项得$-2x\geq - 7 - 1$,即$-2x\geq - 8$,两边同时除以$-2$,不等号方向改变,得$x\leq4$。
3.

4. 原不等式组的解集:
取$x\geq - 3$与$x\leq4$的公共部分,所以原不等式组的解集为$-3\leq x\leq4$。
故答案依次为:
(1)$x\geq - 3$;
(2)$x\leq4$;
(4)$-3\leq x\leq4$。
12. 解不等式组$\left\{\begin{array}{l} 3x + 2 < 2(x + 2),①\\ \frac{x - 1}{2} \leq \frac{2x - 1}{3},②\end{array} \right. $并把它的解集在数轴上表示出来.


答案:
解:
解不等式$①$:
$3x + 2 < 2(x + 2)$
$3x + 2 < 2x + 4$
$3x - 2x < 4 - 2$
$x < 2$
解不等式$②$:
$\frac{x - 1}{2} \leq \frac{2x - 1}{3}$
$3(x - 1) \leq 2(2x - 1)$
$3x - 3 \leq 4x - 2$
$3x - 4x \leq -2 + 3$
$-x \leq 1$
$x \geq -1$
所以不等式组的解集为$-1 \leq x < 2$。
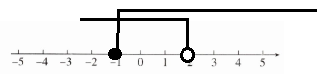
综上,答案为$-1 \leq x < 2$。
解:
解不等式$①$:
$3x + 2 < 2(x + 2)$
$3x + 2 < 2x + 4$
$3x - 2x < 4 - 2$
$x < 2$
解不等式$②$:
$\frac{x - 1}{2} \leq \frac{2x - 1}{3}$
$3(x - 1) \leq 2(2x - 1)$
$3x - 3 \leq 4x - 2$
$3x - 4x \leq -2 + 3$
$-x \leq 1$
$x \geq -1$
所以不等式组的解集为$-1 \leq x < 2$。

综上,答案为$-1 \leq x < 2$。
查看更多完整答案,请扫码查看


