《2025年假日数学吉林出版集团股份有限公司七年级数学华师大版》

6. 不等式 $3 - 2x ＜ 7$ 的解集是______.

答案： $ x ＞ - 2 $

7. 下面是两位同学在讨论一个一元一次不等式.

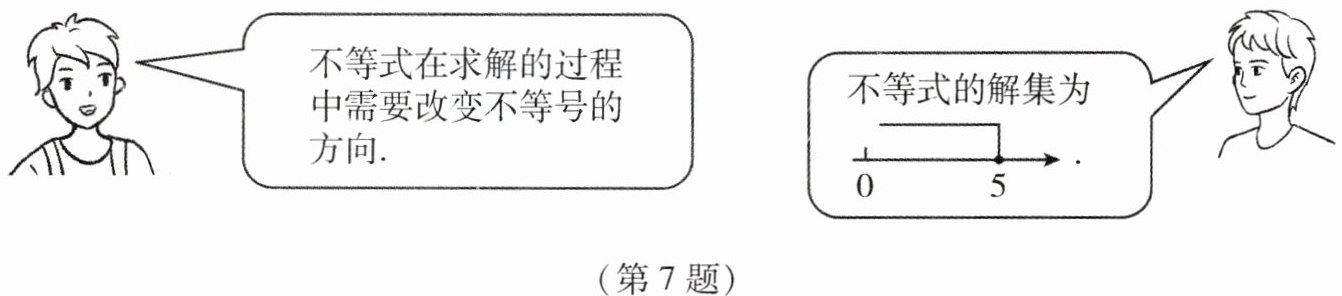
根据上面对话提供的信息,他们讨论的不等式可以是______. (写出一个符合题意的不等式即可)

答案： $ - 2 x \geq - 10 $（答案不唯一）

8. 糯米做成年糕的过程中,由于增加水分,会使得质量增加 20%. 现有糯米 $x$ kg,做成年糕后质量超过 50 kg,则可列出不等式：______.

答案： $ ( 1 + 20 \% ) x ＞ 50 $

9. 小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作,请根据图中给出的信息分析,量筒中至少放入______个小球时有水溢出.

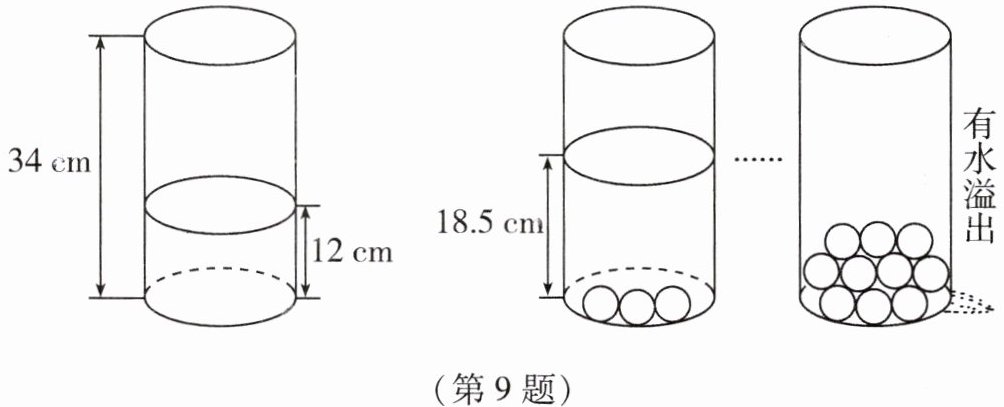
答案： 11

10. 已知 $x = 4$ 是关于 $x$ 的方程 $kx + b = 0(k \neq 0、b ＞ 0)$ 的解,则关于 $x$ 的不等式 $k(x - 3) + b ＞ 0$ 的解集是______.

答案： $ x ＜ 7 $

11. 解不等式 $\frac{1 - x}{6} + 3 ＞ \frac{x + 1}{2}$,并把它的解集在数轴上表示出来,再写出它的所有正整数解.

答案： 解：
1. 首先去分母：
给不等式$\frac{1 - x}{6}+3\gt\frac{x + 1}{2}$两边同时乘以$6$，根据不等式性质$2$（不等式两边同时乘（或除以）同一个大于$0$的整式，不等号方向不变），得到$(1 - x)+18\gt3(x + 1)$。
2. 然后去括号：
根据去括号法则$a+(b + c)=a + b + c$，$a(b + c)=ab+ac$，则$1 - x+18\gt3x + 3$。
3. 接着移项：
把含$x$的项移到一边，常数项移到另一边，根据不等式性质$1$（不等式两边同时加或减去同一个整式，不等号方向不变），得到$-x-3x\gt3 - 1 - 18$。
4. 再合并同类项：
对于$-x-3x\gt3 - 1 - 18$，左边$-x-3x=-4x$，右边$3 - 1 - 18=-16$，即$-4x\gt - 16$。
5. 最后系数化为$1$：
两边同时除以$-4$，根据不等式性质$3$（不等式两边同时乘（或除以）同一个小于$0$的整式，不等号方向改变），得到$x\lt4$。
数轴表示：画一条数轴，找到$4$这个点，用空心圆圈表示（因为$x\lt4$，不包含$4$），然后向左画一条线表示$x$的取值范围。
正整数解：小于$4$的正整数有$1$，$2$，$3$。
所以不等式的解集为$x\lt4$，正整数解为$1$，$2$，$3$。