《2025年假日数学吉林出版集团股份有限公司七年级数学华师大版》

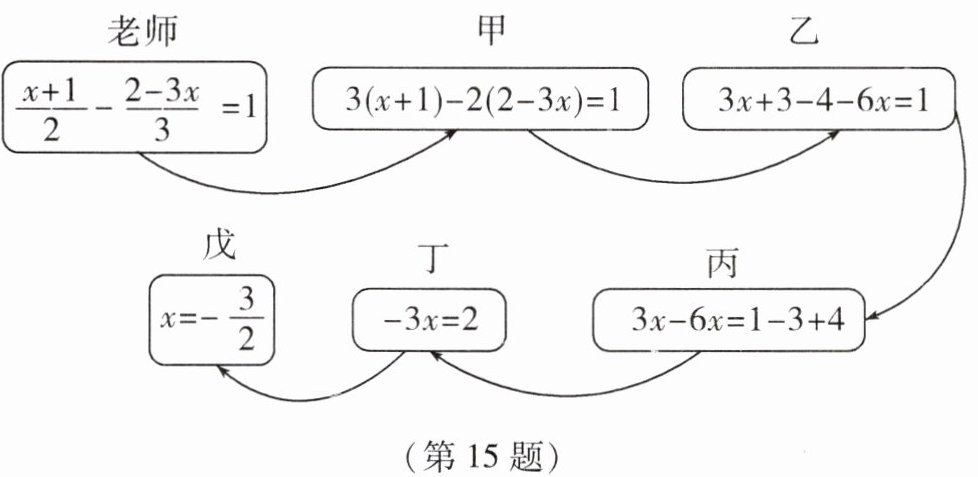
15. 综合实践课上,同学们玩“接力游戏”,由每组学生合作解一元一次方程. 如图,老师将题目交给甲同学,他完成一步解答后交给乙同学,依次进行,最后由戊同学完成求解. 规则是每人只能看到前一人传过来的式子.
(1)写出这个“接力游戏”中过程出错的同学；
(2)请你写出正确的求解过程.

答案： $(1)$找出过程出错的同学
根据去分母、去括号、移项、合并同类项、系数化为$1$的规则来判断：
甲同学：去分母，方程两边同时乘以$6$，$\frac{x + 1}{2}×6-\frac{2 - 3x}{3}×6 = 1×6$，得到$3(x + 1)-2(2 - 3x)=6$，而甲同学得到$3(x + 1)-2(2 - 3x)=1$，所以甲同学出错。
乙同学：根据甲同学错误的式子去括号$3(x + 1)-2(2 - 3x)=1$，得到$3x+3 - 4 + 6x=1$（去括号法则：$a(b+c)=ab+ac$），而乙同学得到$3x + 3-4 - 6x=1$，所以乙同学出错。
所以过程出错的同学是甲、乙。
$(2)$正确的求解过程
解：
去分母：
方程$\frac{x + 1}{2}-\frac{2 - 3x}{3}=1$两边同时乘以$6$（$2$和$3$的最小公倍数），根据等式性质$2$：等式两边同时乘同一个数，等式仍然成立，得到$3(x + 1)-2(2 - 3x)=6$。
去括号：
根据去括号法则$a(b + c)=ab+ac$，$3(x + 1)-2(2 - 3x)=6$可化为$3x+3-4 + 6x=6$。
移项：
把含$x$的项移到等号左边，常数项移到等号右边，根据等式性质$1$：等式两边同时加或减同一个数，等式仍然成立，得到$3x+6x=6-3 + 4$。
合并同类项：
等号左边$3x+6x=(3 + 6)x=9x$，等号右边$6-3 + 4=7$，即$9x=7$。
系数化为$1$：
方程两边同时除以$9$，根据等式性质$2$，得到$x=\frac{7}{9}$。
综上，$(1)$ 过程出错的同学是$\boldsymbol{甲、乙}$；$(2)$ 方程的解为$\boldsymbol{x=\frac{7}{9}}$ 。

16. 今年春节期间,电影《哪吒之魔童闹海》特别火爆,小强一家去某电影院观看此部电影. 到了影院后,看到有以下优惠活动方案：
|优惠方案一|会员费$200$元,票价$35$元/人.|
|优惠方案二|原票价$50$元/人,成人原价,学生票价是原价的$5$折.|
(1)若小强一家$6$人(成人$4$人,学生$2$人),他选择哪种优惠方案划算？
(2)若成人人数是学生人数的$2$倍,且两种优惠方案所付费用相等,求成人、学生各多少人.

答案：
(1)优惠方案二更划算.
(2)学生人数为10人，成人人数为20人.