第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
6. 已知$a > b$,则$-4a$____$-4b$. (填“$<$”“$>$”或“$=$”)
答案:
6. <
7. 已知$x < y$,则$3x + 1$____$3y + 1$. (填“$<$”“$>$”或“$=$”)
答案:
7. <
8. 写出下列各图所表示的不等式的解集:
(1)图①:____;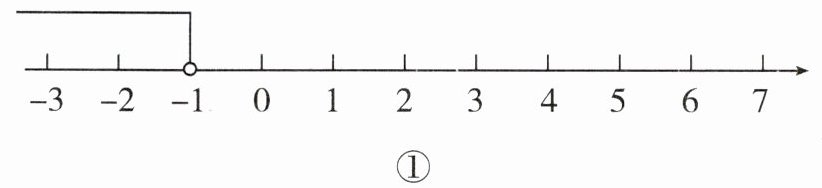
(2)图②:____;
(3)图③:____.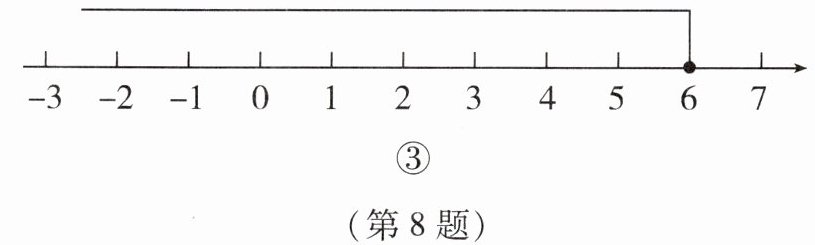
(1)图①:____;

(2)图②:____;

(3)图③:____.

答案:
8.
(1) $ x < - 1 $
(2) $ x > - 2 $
(3) $ x \leq 6 $
(1) $ x < - 1 $
(2) $ x > - 2 $
(3) $ x \leq 6 $
9. 若$x < 3的所有解都能使不等式2x - 1 < m$成立,则$m$的取值范围是____.
答案:
9. $ m \geq 5 $
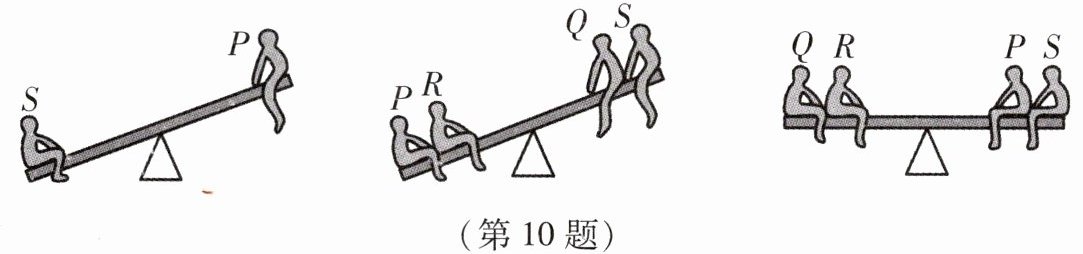
10. 如图,有$P$、$Q$、$R$、$S$四个小朋友去公园玩跷跷板,则这四个小朋友中,最重的是____.

答案:
10. $ R $
11. 已知$x < y$,试比较$6 + 27x和6 + 27y$的大小,并说明理由.
将下面的解题过程补充完整.
解:$6 + 27x$____$6 + 27y$,
理由如下:$\because x < y$,
$\therefore$____(不等式的基本性质$2$),
$\therefore$____(不等式的基本性质$1$).
将下面的解题过程补充完整.
解:$6 + 27x$____$6 + 27y$,
理由如下:$\because x < y$,
$\therefore$____(不等式的基本性质$2$),
$\therefore$____(不等式的基本性质$1$).
答案:
11. < $ 27 x < 27 y $ $ 6 + 27 x < 6 + 27 y $
查看更多完整答案,请扫码查看


