第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
杆秤的起源与发展
杆秤是一种古老的测量工具,其历史可以追溯到几千年前。根据古书记载,早在四五千年前,我们的祖先就已经发明了天平,这是杆秤的前身。这些古代天平通常由一根木制或青铜制的秤杆组成,秤杆的中心系着提绳,两端各有一个秤盘,一个用于放置待称物品,另一个用于放置砝码。这种天平被称为等臂杆秤,因为秤杆上的两个臂长度相等,需要使用与被称物品质量相等的砝码,这在称量较重的物品时显得非常不便。
到了两千多年前,人们发现了不等臂秤的原理,这是一种更为巧妙的方法,只需一个质量固定的秤砣即可称量较重的物品。不等臂秤的特点是秤杆上有尺寸刻度,挂物品的绳子和挂秤砣的绳子都可以在秤杆上移动,从而大大简化了称量过程。
杆秤的结构经历了逐步演化的过程。最初的衡器如战国时期楚国制造的小型衡器——木衡和铜环权,主要用于称量黄金货币。随着时间的推移,衡杆的重臂逐渐缩短,力臂加长,最终演变成了我们今天所熟知的杆秤。
杆秤不仅是一种实用的测量工具,还蕴含着深厚的文化意义。相传,秤是由范蠡受星宿启发而创作出的,一颗星代表一两重,十三颗星代表一斤。为了告诫同行,他将白木刻黑星改为红木嵌金属星形,并在南斗六星和北斗七星之外,再加上福、禄、寿三星,以十六两为一斤。因此,秤这种计量工具便一代一代地流传了下来,并一直沿袭了两千多年,直至今天。
杆秤在公元前由游牧部落传入了西方,被命名为罗马秤。在许多拉丁语作家的著作中都有关于这种秤的记载。罗马秤的设计与中国的杆秤相似,具有不等臂的特点,使得它可以称量比秤锤重得多的物体。
尽管现代科技已经发展出了更加精确和便捷的测量工具,如指针式弹簧秤、电子秤等,但杆秤作为一种传统的测量工具,仍然在某些场合使用。同时,杆秤的设计原理——杠杆原理,仍然是现代测量工具的基础之一。
杆秤的历史是一部科技进步和文化交流的缩影,它见证了人类社会的发展和智慧的积累。从古代的天平到现代的电子秤,杆秤的演变过程展示了人类对测量技术不断追求精确和便捷的努力。
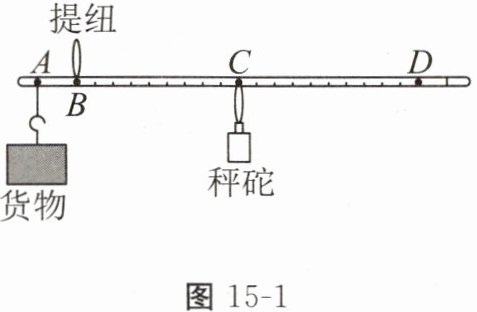
1. 杆秤曾是主要的度量工具,同时它还承载着公平公正的象征意义。某科技小组的同学用轻质细杆制作了一个杆秤,如图15-1所示,$AB= 5cm$,$AD= 55cm$,秤砣的质量为$0.5kg$。使用时将货物挂在秤钩上,用手提起B处的提纽,移动秤砣在秤杆上的位置,当秤杆水平平衡时,可读出货物的质量。秤砣最远可移至D点。秤杆和秤钩的质量忽略不计。下列说法正确的是()。
A. 杆秤的实质是省力杠杆
B. 杆秤D点应标定出的刻度值为$5.5kg$
C. 如果要增大杆秤的量程可将提纽B向A点移动
D. 如果秤砣磨损一部分,用它称得的物体质量小于物体的实际质量
2. 受《天工开物》中桔槔汲水(图15-2甲)启发,某小组自制了“杠杆密度计”,如图乙所示。将一轻质细硬杆用细线固定在O点并悬挂起来,物块固定悬挂在A点,不计质量的矿泉水瓶装满水后用细线悬挂在硬杆上,将悬挂点移至B点时硬杆在水平位置平衡。换用相同的矿泉水瓶装满不同液体,重复以上操作,在杆上可标出悬挂点$B_{1}$、$B_{2}$、$B_{3}$……对应液体密度的刻度值。

(1)若$B_{1}$点在B点的左侧,则$B_{1}点对应的密度\rho_{1}与水的密度\rho_{水}的关系是\rho_{1}$____(选填“<”“=”或“>”)$\rho_{水}$。
(2)若测得B、$B_{2}$到O点的距离分别为$l$、$l_{2}$,则$B_{2}$点标注的密度值为____(用$\rho_{水}$及题中所给字母表示)。
杆秤是一种古老的测量工具,其历史可以追溯到几千年前。根据古书记载,早在四五千年前,我们的祖先就已经发明了天平,这是杆秤的前身。这些古代天平通常由一根木制或青铜制的秤杆组成,秤杆的中心系着提绳,两端各有一个秤盘,一个用于放置待称物品,另一个用于放置砝码。这种天平被称为等臂杆秤,因为秤杆上的两个臂长度相等,需要使用与被称物品质量相等的砝码,这在称量较重的物品时显得非常不便。
到了两千多年前,人们发现了不等臂秤的原理,这是一种更为巧妙的方法,只需一个质量固定的秤砣即可称量较重的物品。不等臂秤的特点是秤杆上有尺寸刻度,挂物品的绳子和挂秤砣的绳子都可以在秤杆上移动,从而大大简化了称量过程。
杆秤的结构经历了逐步演化的过程。最初的衡器如战国时期楚国制造的小型衡器——木衡和铜环权,主要用于称量黄金货币。随着时间的推移,衡杆的重臂逐渐缩短,力臂加长,最终演变成了我们今天所熟知的杆秤。
杆秤不仅是一种实用的测量工具,还蕴含着深厚的文化意义。相传,秤是由范蠡受星宿启发而创作出的,一颗星代表一两重,十三颗星代表一斤。为了告诫同行,他将白木刻黑星改为红木嵌金属星形,并在南斗六星和北斗七星之外,再加上福、禄、寿三星,以十六两为一斤。因此,秤这种计量工具便一代一代地流传了下来,并一直沿袭了两千多年,直至今天。
杆秤在公元前由游牧部落传入了西方,被命名为罗马秤。在许多拉丁语作家的著作中都有关于这种秤的记载。罗马秤的设计与中国的杆秤相似,具有不等臂的特点,使得它可以称量比秤锤重得多的物体。
尽管现代科技已经发展出了更加精确和便捷的测量工具,如指针式弹簧秤、电子秤等,但杆秤作为一种传统的测量工具,仍然在某些场合使用。同时,杆秤的设计原理——杠杆原理,仍然是现代测量工具的基础之一。
杆秤的历史是一部科技进步和文化交流的缩影,它见证了人类社会的发展和智慧的积累。从古代的天平到现代的电子秤,杆秤的演变过程展示了人类对测量技术不断追求精确和便捷的努力。
1. 杆秤曾是主要的度量工具,同时它还承载着公平公正的象征意义。某科技小组的同学用轻质细杆制作了一个杆秤,如图15-1所示,$AB= 5cm$,$AD= 55cm$,秤砣的质量为$0.5kg$。使用时将货物挂在秤钩上,用手提起B处的提纽,移动秤砣在秤杆上的位置,当秤杆水平平衡时,可读出货物的质量。秤砣最远可移至D点。秤杆和秤钩的质量忽略不计。下列说法正确的是()。

A. 杆秤的实质是省力杠杆
B. 杆秤D点应标定出的刻度值为$5.5kg$
C. 如果要增大杆秤的量程可将提纽B向A点移动
D. 如果秤砣磨损一部分,用它称得的物体质量小于物体的实际质量
2. 受《天工开物》中桔槔汲水(图15-2甲)启发,某小组自制了“杠杆密度计”,如图乙所示。将一轻质细硬杆用细线固定在O点并悬挂起来,物块固定悬挂在A点,不计质量的矿泉水瓶装满水后用细线悬挂在硬杆上,将悬挂点移至B点时硬杆在水平位置平衡。换用相同的矿泉水瓶装满不同液体,重复以上操作,在杆上可标出悬挂点$B_{1}$、$B_{2}$、$B_{3}$……对应液体密度的刻度值。

(1)若$B_{1}$点在B点的左侧,则$B_{1}点对应的密度\rho_{1}与水的密度\rho_{水}的关系是\rho_{1}$____(选填“<”“=”或“>”)$\rho_{水}$。
(2)若测得B、$B_{2}$到O点的距离分别为$l$、$l_{2}$,则$B_{2}$点标注的密度值为____(用$\rho_{水}$及题中所给字母表示)。
答案:
1. C 2.
(1) >
(2) $\frac{l}{l_{2}}\rho_{水}$
(1) >
(2) $\frac{l}{l_{2}}\rho_{水}$
查看更多完整答案,请扫码查看


