第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
【活用6】(1)某大学被宽为h的街道分成两部分(如图①),P为宿舍区,Q为教学区,为了方便师生及过街安全,学校准备架设一座与街道垂直的人行天桥,请你用所学的知识帮助选择桥址,使P,Q之间的路程最短,并说明理由;

如图,过P作PP'⊥a,且使PP'=h,连接P'Q交b于M.过M作MN⊥a于N.连接PN,则在M,N处选址即可.

理由:设N'为a上除N外任一点,过N'作N'M'⊥b于M',连接PN',P'M',M'Q.
由于P'是由P沿垂直于街道方向平移街宽得到,
所以PN'=P'M',PN=P'M.
因为P'M+MQ<P'M'+M'Q(两点之间,线段最短),
所以PN+MQ<PN'+M'Q.
因为NM=N'M',
所以PN+NM+MQ<PN'+N'M'+M'Q.
(2)若该大学被宽分别为m,n的两条平行街道分割成两部分(如图②),P为宿舍区,Q为教学区,准备架设两座天桥,请你帮助选择桥址,使P,Q之间的路程最短(不写理由)。注:以上不考虑其他因素。
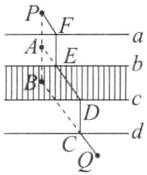
如图,过P作PB⊥直线c,且使PB=m+n,连接BQ交直线d于C点,过C作CD⊥直线c于D,在PB上取A点,使PA=m,连接AD交直线b于E,过E作EF⊥直线a于F,则EF,DC为建桥位置.

如图,过P作PP'⊥a,且使PP'=h,连接P'Q交b于M.过M作MN⊥a于N.连接PN,则在M,N处选址即可.

理由:设N'为a上除N外任一点,过N'作N'M'⊥b于M',连接PN',P'M',M'Q.
由于P'是由P沿垂直于街道方向平移街宽得到,
所以PN'=P'M',PN=P'M.
因为P'M+MQ<P'M'+M'Q(两点之间,线段最短),
所以PN+MQ<PN'+M'Q.
因为NM=N'M',
所以PN+NM+MQ<PN'+N'M'+M'Q.
(2)若该大学被宽分别为m,n的两条平行街道分割成两部分(如图②),P为宿舍区,Q为教学区,准备架设两座天桥,请你帮助选择桥址,使P,Q之间的路程最短(不写理由)。注:以上不考虑其他因素。
如图,过P作PB⊥直线c,且使PB=m+n,连接BQ交直线d于C点,过C作CD⊥直线c于D,在PB上取A点,使PA=m,连接AD交直线b于E,过E作EF⊥直线a于F,则EF,DC为建桥位置.

答案:
[活用6]
(1)如图,过P作PP'⊥a,且使PP'=h,连接P'Q交b于M.过M作MN⊥a于N.连接PN,则在M,N处选址即可.

理由:设N'为a上除N外任一点,过N'作N'M'⊥b于M',连接PN',P'M',M'Q.
由于P'是由P沿垂直于街道方向平移街宽得到,
所以PN'=P'M',PN=P'M.
因为P'M+MQ<P'M'+M'Q(两点之间,线段最短),
所以PN+MQ<PN'+M'Q.
因为NM=N'M',
所以PN+NM+MQ<PN'+N'M'+M'Q.
(2)如图,过P作PB⊥直线c,且使PB=m+n,连接BQ交直线d于C点,过C作CD⊥直线c于D,在PB上取A点,使PA=m,连接AD交直线b于E,过E作EF⊥直线a于F,则EF,DC为建桥位置.

[活用6]
(1)如图,过P作PP'⊥a,且使PP'=h,连接P'Q交b于M.过M作MN⊥a于N.连接PN,则在M,N处选址即可.

理由:设N'为a上除N外任一点,过N'作N'M'⊥b于M',连接PN',P'M',M'Q.
由于P'是由P沿垂直于街道方向平移街宽得到,
所以PN'=P'M',PN=P'M.
因为P'M+MQ<P'M'+M'Q(两点之间,线段最短),
所以PN+MQ<PN'+M'Q.
因为NM=N'M',
所以PN+NM+MQ<PN'+N'M'+M'Q.
(2)如图,过P作PB⊥直线c,且使PB=m+n,连接BQ交直线d于C点,过C作CD⊥直线c于D,在PB上取A点,使PA=m,连接AD交直线b于E,过E作EF⊥直线a于F,则EF,DC为建桥位置.

填哪个数?


6
答案:
【解析】:观察下面两个完整的表格,发现规律是:同一表格中,左上角数字 + 右下角数字 = 右上角数字 + 左下角数字。
第一个完整表格:$2 + 6 = 7 + 1 = 8$;
第二个完整表格:$5 + 2 = 1 + 4 = 7$;
对于第一个表格(有问号的),设问号处数字为$x$,则$7 + x = 8 + 5$,即$7 + x = 13$,解得$x = 13 - 7 = 6$。
【答案】:$6$
第一个完整表格:$2 + 6 = 7 + 1 = 8$;
第二个完整表格:$5 + 2 = 1 + 4 = 7$;
对于第一个表格(有问号的),设问号处数字为$x$,则$7 + x = 8 + 5$,即$7 + x = 13$,解得$x = 13 - 7 = 6$。
【答案】:$6$
查看更多完整答案,请扫码查看


