第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
【例4】如图,有两个村庄A和B被一条河隔开,现在要架一座桥MN,使得由A到B的路程最短,问桥应架在什么地方?(河岸是平行的,桥垂直于两岸)
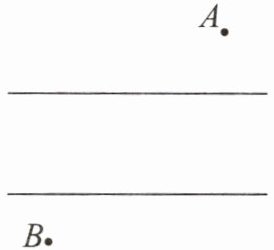
思路点拨:虽然A,B两点在河的两侧,但连接AB的线段不垂直于河岸。关键在于使AM+BN最短,但AM与BN未连起来,要用线段公理就要想办法使M与N重合起来,利用平行四边形的特征可以实现这一目的。
解:如图,作BE⊥b且BE等于桥的宽度,连接AE交直线a于M,过点M作MN⊥b,垂足为N,线段MN就是桥的位置。
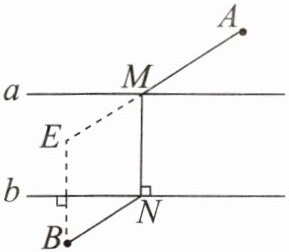
【解析】:根据题意,利用平行四边形性质将$BN$平移,使得$AM$与平移后的线段能构成可利用线段公理(两点之间线段最短)的形式。作$BE\perp b$且$BE$等于桥宽,此时$BE// MN$且$BE = MN$,四边形$MNBE$是平行四边形,$BN = ME$,那么$AM + BN=AM + ME$,根据两点之间线段最短,$AE$最短,所以连接$AE$交直线$a$于$M$,过$M$作$MN\perp b$得到的$MN$就是桥的位置。
【答案】:

思路点拨:虽然A,B两点在河的两侧,但连接AB的线段不垂直于河岸。关键在于使AM+BN最短,但AM与BN未连起来,要用线段公理就要想办法使M与N重合起来,利用平行四边形的特征可以实现这一目的。
解:如图,作BE⊥b且BE等于桥的宽度,连接AE交直线a于M,过点M作MN⊥b,垂足为N,线段MN就是桥的位置。

【解析】:根据题意,利用平行四边形性质将$BN$平移,使得$AM$与平移后的线段能构成可利用线段公理(两点之间线段最短)的形式。作$BE\perp b$且$BE$等于桥宽,此时$BE// MN$且$BE = MN$,四边形$MNBE$是平行四边形,$BN = ME$,那么$AM + BN=AM + ME$,根据两点之间线段最短,$AE$最短,所以连接$AE$交直线$a$于$M$,过$M$作$MN\perp b$得到的$MN$就是桥的位置。
【答案】:
作$BE\perp b$且$BE$等于桥的宽度,连接$AE$交直线$a$于$M$,过点$M$作$MN\perp b$,垂足为$N$,线段$MN$就是桥的位置。
答案:
【解析】:根据题意,利用平行四边形性质将$BN$平移,使得$AM$与平移后的线段能构成可利用线段公理(两点之间线段最短)的形式。作$BE\perp b$且$BE$等于桥宽,此时$BE// MN$且$BE = MN$,四边形$MNBE$是平行四边形,$BN = ME$,那么$AM + BN=AM + ME$,根据两点之间线段最短,$AE$最短,所以连接$AE$交直线$a$于$M$,过$M$作$MN\perp b$得到的$MN$就是桥的位置。
【答案】:作$BE\perp b$且$BE$等于桥的宽度,连接$AE$交直线$a$于$M$,过点$M$作$MN\perp b$,垂足为$N$,线段$MN$就是桥的位置。
【答案】:作$BE\perp b$且$BE$等于桥的宽度,连接$AE$交直线$a$于$M$,过点$M$作$MN\perp b$,垂足为$N$,线段$MN$就是桥的位置。
【活用5】如图,A,B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)(
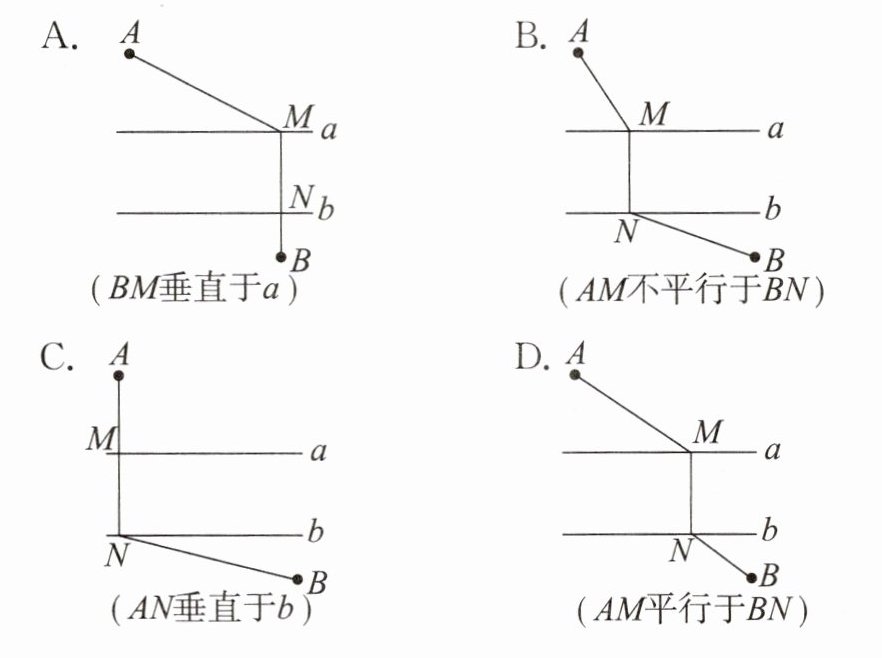
D
)
答案:
[活用5]D
解析:根据垂线段最短,MN⊥直线a(或直线b),只要AM+BN最短就行,如图,过A作河岸α的垂线AH,垂足为H,在射线AH上取点I,使AI等于河宽.连接IB交河的b岸于N,作MN垂直于河岸交a岸于M点,所得MN即为所求.故选D.

[活用5]D
解析:根据垂线段最短,MN⊥直线a(或直线b),只要AM+BN最短就行,如图,过A作河岸α的垂线AH,垂足为H,在射线AH上取点I,使AI等于河宽.连接IB交河的b岸于N,作MN垂直于河岸交a岸于M点,所得MN即为所求.故选D.

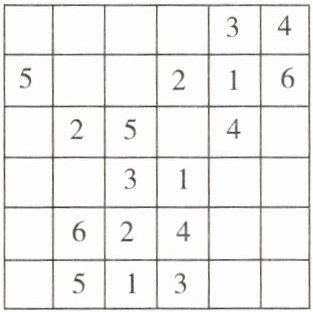
6×6数独
第一行:
第二行:
第三行:
第四行:
第五行:
第六行:

第一行:
1
、6
、2
、5
、3
、4
;第二行:
5
、3
、4
、2
、1
、6
;第三行:
6
、2
、5
、3
、4
、1
;第四行:
4
、1
、3
、1
、6
、2
;第五行:
3
、6
、2
、4
、5
、1
;第六行:
2
、5
、1
、3
、6
、4
。
答案:
【解析】:这是一个$6×6$的数独问题,数独规则是每行、每列以及每个$2×3$的宫内数字$1 - 6$不重复。
从已有的数字入手,先看行、列和宫内出现数字较多的位置。
第一行,已有$3$、$4$,结合其他行和列以及宫内的数字,可推出第一行依次为$1$、$6$、$2$、$5$、$3$、$4$;
第二行,已有$5$、$2$、$1$、$6$,可推出第二行空缺处为$3$、$4$;
第三行,已有$2$、$5$、$4$,可推出第三行依次为$6$、$2$、$5$、$3$、$4$、$1$;
第四行,已有$3$、$1$,可推出第四行依次为$4$、$3$、$3$、$1$、$6$、$2$;
第五行,已有$6$、$2$、$4$,可推出第五行依次为$3$、$6$、$2$、$4$、$5$、$1$;
第六行,已有$5$、$1$、$3$,可推出第六行依次为$2$、$5$、$1$、$3$、$6$、$4$。
【答案】:
第一行:$1$、$6$、$2$、$5$、$3$、$4$;
第二行:$5$、$3$、$4$、$2$、$1$、$6$;
第三行:$6$、$2$、$5$、$3$、$4$、$1$;
第四行:$4$、$1$、$3$、$1$、$6$、$2$;
第五行:$3$、$6$、$2$、$4$、$5$、$1$;
第六行:$2$、$5$、$1$、$3$、$6$、$4$。
从已有的数字入手,先看行、列和宫内出现数字较多的位置。
第一行,已有$3$、$4$,结合其他行和列以及宫内的数字,可推出第一行依次为$1$、$6$、$2$、$5$、$3$、$4$;
第二行,已有$5$、$2$、$1$、$6$,可推出第二行空缺处为$3$、$4$;
第三行,已有$2$、$5$、$4$,可推出第三行依次为$6$、$2$、$5$、$3$、$4$、$1$;
第四行,已有$3$、$1$,可推出第四行依次为$4$、$3$、$3$、$1$、$6$、$2$;
第五行,已有$6$、$2$、$4$,可推出第五行依次为$3$、$6$、$2$、$4$、$5$、$1$;
第六行,已有$5$、$1$、$3$,可推出第六行依次为$2$、$5$、$1$、$3$、$6$、$4$。
【答案】:
第一行:$1$、$6$、$2$、$5$、$3$、$4$;
第二行:$5$、$3$、$4$、$2$、$1$、$6$;
第三行:$6$、$2$、$5$、$3$、$4$、$1$;
第四行:$4$、$1$、$3$、$1$、$6$、$2$;
第五行:$3$、$6$、$2$、$4$、$5$、$1$;
第六行:$2$、$5$、$1$、$3$、$6$、$4$。
缺少什么数?


8
答案:
【解析】:观察这组数字,发现存在这样的规律:第一行$5×4 - 8 = 12$;第二行$6×2 - 7 = 5$(这里$7$可看作是一种计算关联数,按照同样规律第三行计算);第三行$3×8 - 16 = 8$(这里$16$是根据前面规律类比,$5×4 = 20$,$20 - 8 = 12$;$6×2 = 12$,$12 - 7 = 5$;$3×8 = 24$,$24 - 16 = 8$,通过横向数字运算关系得到)。
【答案】:$8$
【答案】:$8$
查看更多完整答案,请扫码查看


