第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
专题2 巧妙运用截长补短的方法解决问题
例2 如图,在△ABC中,AC>BC,CD是△ABC的平分线.求证:AC-BC>AD-BD.
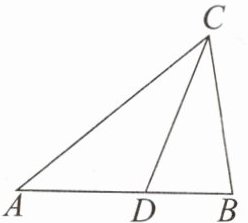
【解析】解决本题的关键是如何把AC-BC与AD,BD联系在一起,结论AC-BC>AD-BD是线段之间的不等关系,所以考虑利用“三角形两边之和大于第三边”这一性质,如何把这些分散的条件集中到一个三角形里呢?注意到角平分线的对称性,考虑通过角平分线构造全等三角形.在AC上截取CE= BC,连接DE,可证得△CDE≌△CDB,从而将BC,BD转移到CE,DE的位置,这时AC-BC转化成AE,再利用△ADE三边不等关系可解决问题.
【答案】∵AC>BC,∴可在AC上截取CE= BC,连接DE,如图.
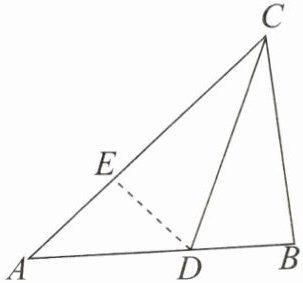
∵CD是△ABC的平分线,∠DCA= ∠DCB.
在△CDE与△CDB中, $\left\{ \begin{array} { l } { C E = C B , ( \text { 已作 } ) } \\ { \angle D C A = \angle D C B , ( \text { 已证 } ) } \\ { C D = C D , ( \text { 公共边 } ) } \end{array} \right.$
∴△CDE≌△CDB(SAS),
∴BC= CE,BD= DE,
∴AC-BC= AC-CE= AE.
在△ADE中,AE>AD-DE,
∴AC-BC>AD-BD.
【点拨】本题并没有利用角平分线的性质解题,而是利用角平分线的定义采用截长补短的方法构造全等三角形,将分散的条件转移到一个基本图形中.这种截长补短的方法也是有关角平分线问题中常见的辅助线作法,应予以掌握.
例2 如图,在△ABC中,AC>BC,CD是△ABC的平分线.求证:AC-BC>AD-BD.

【解析】解决本题的关键是如何把AC-BC与AD,BD联系在一起,结论AC-BC>AD-BD是线段之间的不等关系,所以考虑利用“三角形两边之和大于第三边”这一性质,如何把这些分散的条件集中到一个三角形里呢?注意到角平分线的对称性,考虑通过角平分线构造全等三角形.在AC上截取CE= BC,连接DE,可证得△CDE≌△CDB,从而将BC,BD转移到CE,DE的位置,这时AC-BC转化成AE,再利用△ADE三边不等关系可解决问题.
【答案】∵AC>BC,∴可在AC上截取CE= BC,连接DE,如图.

∵CD是△ABC的平分线,∠DCA= ∠DCB.
在△CDE与△CDB中, $\left\{ \begin{array} { l } { C E = C B , ( \text { 已作 } ) } \\ { \angle D C A = \angle D C B , ( \text { 已证 } ) } \\ { C D = C D , ( \text { 公共边 } ) } \end{array} \right.$
∴△CDE≌△CDB(SAS),
∴BC= CE,BD= DE,
∴AC-BC= AC-CE= AE.
在△ADE中,AE>AD-DE,
∴AC-BC>AD-BD.
【点拨】本题并没有利用角平分线的性质解题,而是利用角平分线的定义采用截长补短的方法构造全等三角形,将分散的条件转移到一个基本图形中.这种截长补短的方法也是有关角平分线问题中常见的辅助线作法,应予以掌握.
答案:
【答案】
∵AC>BC,
∴可在AC上截取CE= BC,连接DE,如图.

∵CD是△ABC的平分线,∠DCA= ∠DCB.
在△CDE与△CDB中, $\left\{ \begin{array} { l } { C E = C B , ( \text { 已作 } ) } \\ { \angle D C A = \angle D C B , ( \text { 已证 } ) } \\ { C D = C D , ( \text { 公共边 } ) } \end{array} \right.$
∴△CDE≌△CDB(SAS),
∴BC= CE,BD= DE,
∴AC-BC= AC-CE= AE.
在△ADE中,AE>AD-DE,
∴AC-BC>AD-BD.
【点拨】本题并没有利用角平分线的性质解题,而是利用角平分线的定义采用截长补短的方法构造全等三角形,将分散的条件转移到一个基本图形中.这种截长补短的方法也是有关角平分线问题中常见的辅助线作法,应予以掌握.
【答案】
∵AC>BC,
∴可在AC上截取CE= BC,连接DE,如图.

∵CD是△ABC的平分线,∠DCA= ∠DCB.
在△CDE与△CDB中, $\left\{ \begin{array} { l } { C E = C B , ( \text { 已作 } ) } \\ { \angle D C A = \angle D C B , ( \text { 已证 } ) } \\ { C D = C D , ( \text { 公共边 } ) } \end{array} \right.$
∴△CDE≌△CDB(SAS),
∴BC= CE,BD= DE,
∴AC-BC= AC-CE= AE.
在△ADE中,AE>AD-DE,
∴AC-BC>AD-BD.
【点拨】本题并没有利用角平分线的性质解题,而是利用角平分线的定义采用截长补短的方法构造全等三角形,将分散的条件转移到一个基本图形中.这种截长补短的方法也是有关角平分线问题中常见的辅助线作法,应予以掌握.
查看更多完整答案,请扫码查看


