第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
广告征集
图案设计征集
学校艺术教室要做内部装修,现向广大同学及全体教职员工征集地面装饰图案,具体要求如下:
一、整个地面图案由一种多边形的不同方式的组合经平移后而成。
二、设计要新颖,给人新奇感。
三、线条要简单,以便于施工。
四、画出多边形图案并说明如何镶嵌及理论根据。
有意者请于十日内把作品交到学校后勤办公室。
学校后勤办公室
3月16日
同学们见到征集广告后,认为我们刚刚学完了平面镶嵌的内容,都想检验自己解决实际问题的能力,踊跃参加了这项活动,学校后勤处收到了大量的学生作品,其中部分作品如下。
作品展示
作品一 利用下图的不等边三角形图案镶嵌整个地面。

可行性分析:
1. 常见的地面砖都是正方形的,镶嵌的地面图形比较呆板,现在用三角形的图案镶嵌地面,组成的图形一定有新奇感,但是三角形的图案是否能铺满整个地面呢?它要符合一个条件:一般地,图案中有公共顶点的角的和必须是

2. 上页图可以由下面图中三个组合图形中的各一个平移而得到。

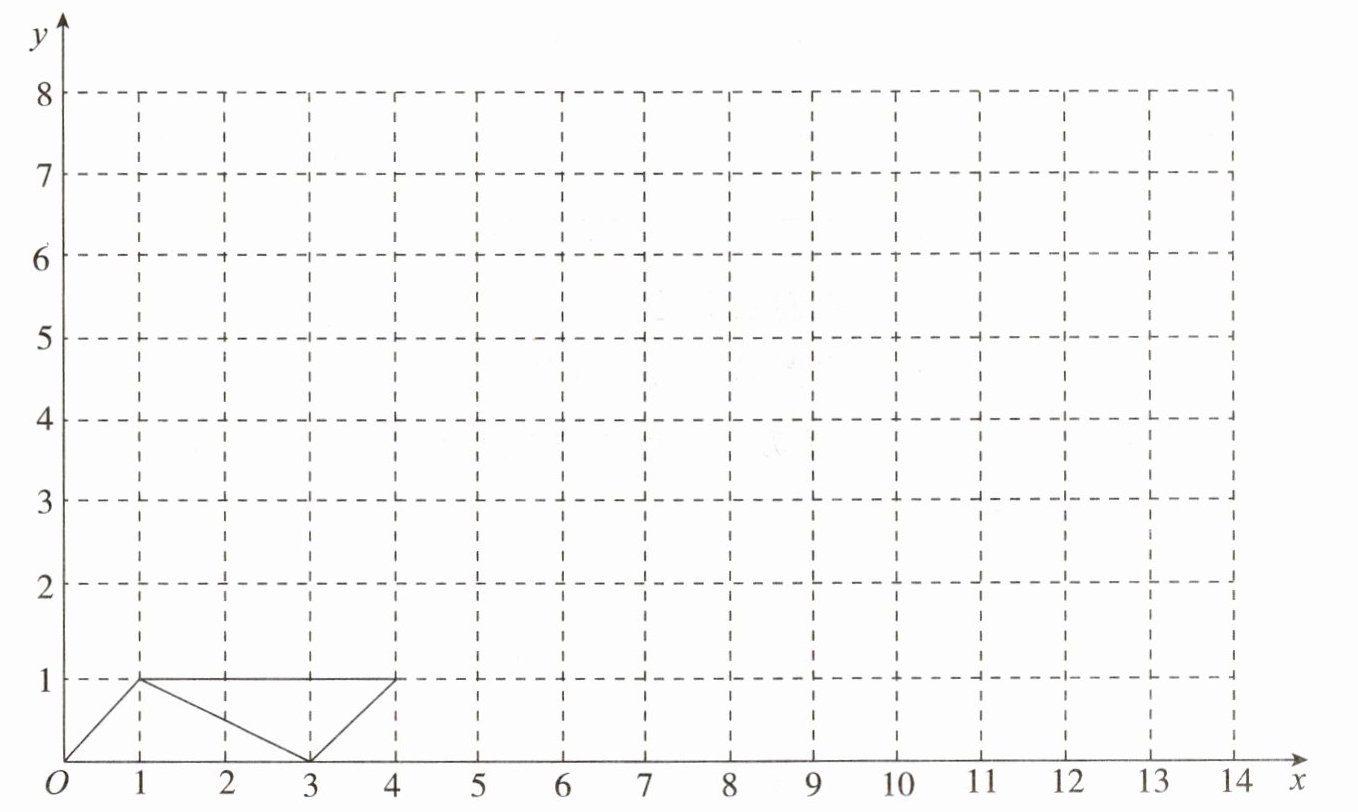
3. 在下面的平面直角坐标系内,平移图①看是否能达到镶嵌平面的目的。
标出坐标系内这个四边形四个顶点的坐标,它们依次是
4. 在下图的平面直角坐标系内平行移动图③铺满平面。
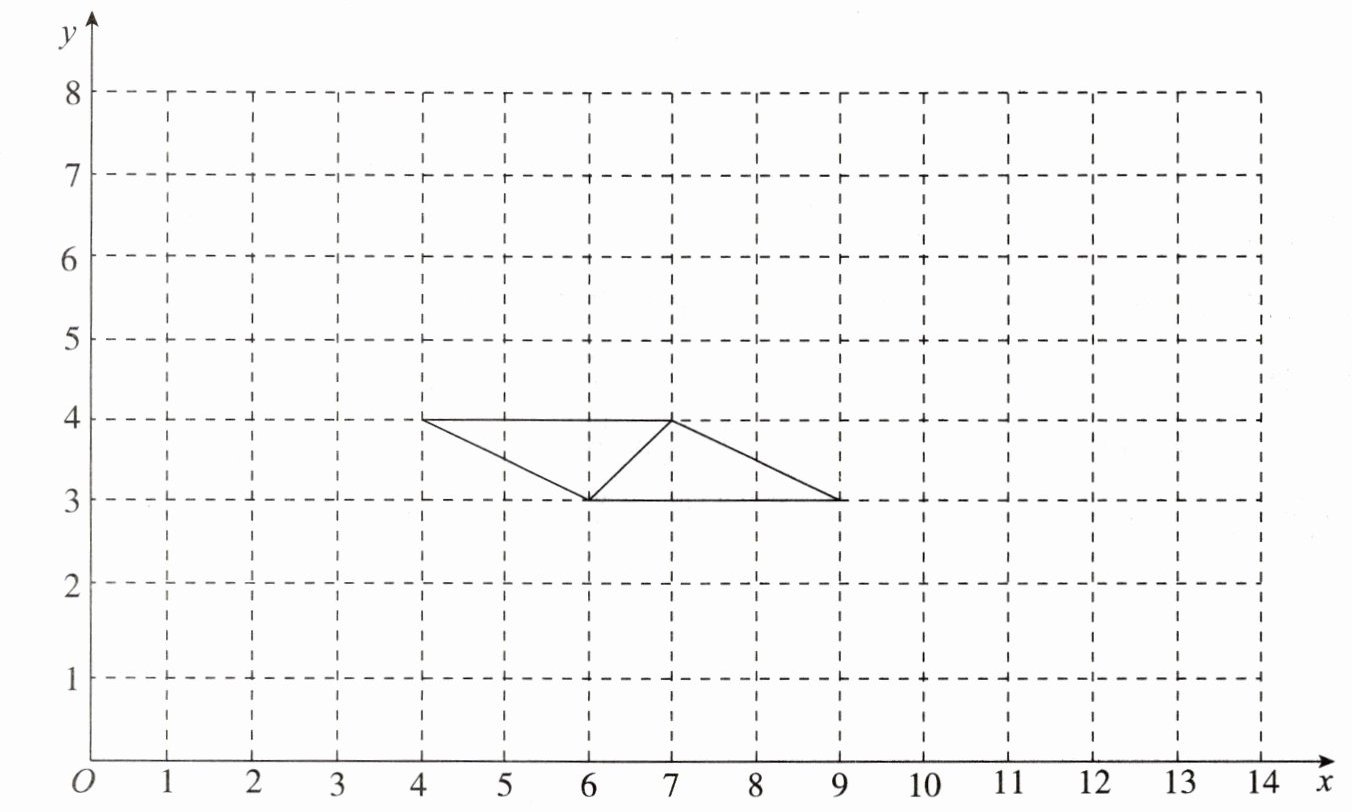
标出这个四边形四个顶点的坐标,它们依次是
图案设计征集
学校艺术教室要做内部装修,现向广大同学及全体教职员工征集地面装饰图案,具体要求如下:
一、整个地面图案由一种多边形的不同方式的组合经平移后而成。
二、设计要新颖,给人新奇感。
三、线条要简单,以便于施工。
四、画出多边形图案并说明如何镶嵌及理论根据。
有意者请于十日内把作品交到学校后勤办公室。
学校后勤办公室
3月16日
同学们见到征集广告后,认为我们刚刚学完了平面镶嵌的内容,都想检验自己解决实际问题的能力,踊跃参加了这项活动,学校后勤处收到了大量的学生作品,其中部分作品如下。
作品展示
作品一 利用下图的不等边三角形图案镶嵌整个地面。

可行性分析:
1. 常见的地面砖都是正方形的,镶嵌的地面图形比较呆板,现在用三角形的图案镶嵌地面,组成的图形一定有新奇感,但是三角形的图案是否能铺满整个地面呢?它要符合一个条件:一般地,图案中有公共顶点的角的和必须是
$ 360 ^ { \circ } $
,三角形三个内角的和是$ 180 ^ { \circ } $
。如果六个角合在一起就能满足这个条件,如图。
2. 上页图可以由下面图中三个组合图形中的各一个平移而得到。

3. 在下面的平面直角坐标系内,平移图①看是否能达到镶嵌平面的目的。
标出坐标系内这个四边形四个顶点的坐标,它们依次是
$ ( 1, 1 ) $,$ ( 0, 0 ) $,$ ( 3, 0 ) $,$ ( 4, 1 ) $
,把四边形向右平移3个单位长度,画出图形并标出顶点坐标$ ( 4, 1 ) $,$ ( 3, 0 ) $,$ ( 6, 0 ) $,$ ( 7, 1 ) $
,再把它依次向右平行移动;然后把移动后得到的整个图形向上平行移动多次,每次移动1个单位长度。
4. 在下图的平面直角坐标系内平行移动图③铺满平面。

标出这个四边形四个顶点的坐标,它们依次是
$ ( 4, 4 ) $,$ ( 6, 3 ) $,$ ( 9, 3 ) $,$ ( 7, 4 ) $
。把四边形向下平移1个长度单位,画出图形并标出顶点坐标$ ( 4, 3 ) $,$ ( 6, 2 ) $,$ ( 9, 2 ) $,$ ( 7, 3 ) $
;然后把移动后得到的整个图形向四个方向平行移动直到铺满整个平面,并欣赏你的作品。综上可知这个设计能够铺满地面。
答案:
1. $ 360 ^ { \circ } $,$ 180 ^ { \circ } $ 3. (图略)$ ( 1, 1 ) $,$ ( 0, 0 ) $,$ ( 3, 0 ) $,$ ( 4, 1 ) $ $ ( 4, 1 ) $,$ ( 3, 0 ) $,$ ( 6, 0 ) $,$ ( 7, 1 ) $ 4. (图略)$ ( 4, 4 ) $,$ ( 6, 3 ) $,$ ( 9, 3 ) $,$ ( 7, 4 ) $ $ ( 4, 3 ) $,$ ( 6, 2 ) $,$ ( 9, 2 ) $,$ ( 7, 3 ) $
查看更多完整答案,请扫码查看


