《2025年新课程暑假作业本七年级综合A版山西教育出版社》

2. 如图所示的正方形网格,小正方形的顶点称为格点.点 A,B,C 均在格点上,只用无刻度的直尺在给定的网格中按要求画图,不要求写作法.

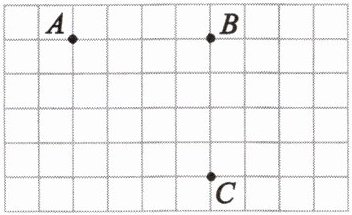
(1) 画射线 AC;
(2) 过点 B 画 AC 的平行线 BD(点 D 在格点上);
(3) 在射线 AC 上取一点 E,画线段 BE,使其长度表示点 B 到 AC 的距离.

答案：

(1) 如图，射线AC即为所求；
(2) 如图，直线BD即为所求；
(3) 如图，线段BE即为所求.

3. 如图,$AB// DC$,AE 平分$∠BAD$,CD 与 AE 相交于点 F,$∠CFE=∠E$,试说明$AD// BC$.

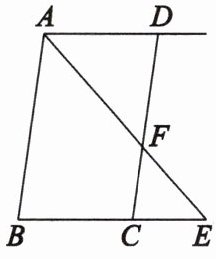
解：∵ AB // DC，
∴ ∠BAE = ∠CFE.
∵ AE 平分 ∠BAD，
∴ ∠BAE = ∠DAE.
∴ ∠DAE = ∠CFE.
∵ ∠CFE = ∠E，
∴ ∠DAE = ∠E.
∴ AD // BC.

答案： $ ∵ AB // DC $，
$ ∴ ∠BAE = ∠CFE $.
$ ∵ AE $ 平分 $ ∠BAD $，
$ ∴ ∠BAE = ∠DAE $.
$ ∴ ∠DAE = ∠CFE $.
$ ∵ ∠CFE = ∠E $，
$ ∴ ∠DAE = ∠E $.
$ ∴ AD // BC $.

4. 在综合与实践课上,老师组织七年级(2)班的同学开展了“探究两角之间数量关系”的数学活动.如图,射线$AM// BN$,连接 AB,P 是射线 AM 上的一个动点(不与点 A 重合),BC 平分$∠ABP$,BD 平分$∠PBN$,分别交射线 AM 于点 C,D.

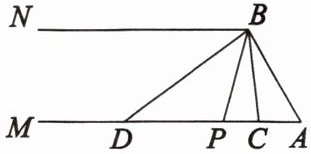
(1) ①“快乐小组”经过探索后发现:当$∠A=60^{\circ }$时,$∠CBD=∠A$.请说明理由;
②不断改变$∠A$的度数,$∠CBD$与$∠A$始终满足某种数量关系,直接写出用$∠A$表示$∠CBD$的式子:$∠CBD = \frac{180^{\circ} - ∠A}{2}$.
(2) ①“智慧小组”利用量角器量出$∠APB$和$∠ADB$的度数后,探究二者满足的数量关系.他们发现,当点 P 在射线 AM 上运动时,无论点 P 在 AM 上的什么位置,$∠APB$与$∠ADB$满足的数量关系都保持不变,请写出它们满足的数量关系式:$∠APB = 2∠ADB$,并说明理由;
②点 P 在射线 AM 上运动,当运动到$∠ACB=∠ABD$时,请直接写出$2∠ABC+\frac {1}{2}∠A$的结果:$90^{\circ}$.

答案：
(1) ① $ ∵ AM // BN $，
$ ∴ ∠A + ∠ABN = 180^{\circ} $.
$ ∵ ∠A = 60^{\circ} $，
$ ∴ ∠ABN = 120^{\circ} $.
$ ∵ BC $ 平分 $ ∠ABP $，$ BD $ 平分 $ ∠PBN $，
$ ∴ ∠CBP = \frac{1}{2}∠ABP $，$ ∠DBP = \frac{1}{2}∠PBN $，
$ ∴ ∠CBD = ∠CBP + ∠DBP = \frac{1}{2}∠ABP + \frac{1}{2}∠PBN = \frac{1}{2}∠ABN = 60^{\circ} $，
$ ∴ ∠CBD = ∠A $.
② $ ∠CBD = \frac{180^{\circ} - ∠A}{2} $
(2) ① $ ∠APB = 2∠ADB $. 理由如下：
$ ∵ BD $ 平分 $ ∠PBN $，
$ ∴ ∠PBN = 2∠NBD $.
$ ∵ AM // BN $，
$ ∴ ∠APB = ∠PBN $，$ ∠ADB = ∠NBD $，
$ ∴ ∠APB = 2∠ADB $.
② $ 2∠ABC + \frac{1}{2}∠A = 90^{\circ} $