2025年书香天博暑假作业五年级数学北师大版西安出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年书香天博暑假作业五年级数学北师大版西安出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
4. 右图是由8个小正方体拼成的,如果拿走1个小正方体,它的表面积和原来相比( )。

A.变小了
B.变大了
C.没有变化

A.变小了
B.变大了
C.没有变化
答案:
解析:由图可知,拿走位于顶点处的小正方体,减少了小正方体的3个面,同时又露出了小正方体的3个面,所以表面积和原来相比没有变化。
答案:C
答案:C
四、看图列式(或方程)并计算。
1.

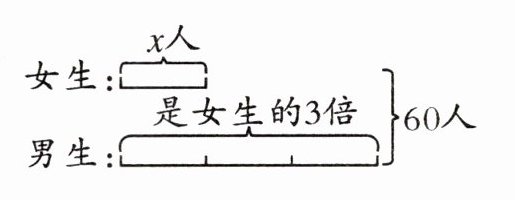
2.

1.

2.
答案:
1.
解析:从图中可知,总重量$x$吨,其中$\frac{3}{5}$对应的重量是$60$吨,可据此列出方程求解总重量。
方程:$\frac{3}{5}x = 60$
计算过程:
$x=60÷\frac{3}{5}$
$x = 60×\frac{5}{3}$
$x = 100$
答案:$x = 100$
2.
解析:从图中可知,女生人数为$x$人,男生人数是女生的$3$倍,即$3x$人,男女生总人数为$60$人,可据此列出方程求解女生人数。
方程:$x + 3x = 60$
计算过程:
$4x = 60$
$x = 60÷4$
$x = 15$
答案:$x = 15$
解析:从图中可知,总重量$x$吨,其中$\frac{3}{5}$对应的重量是$60$吨,可据此列出方程求解总重量。
方程:$\frac{3}{5}x = 60$
计算过程:
$x=60÷\frac{3}{5}$
$x = 60×\frac{5}{3}$
$x = 100$
答案:$x = 100$
2.
解析:从图中可知,女生人数为$x$人,男生人数是女生的$3$倍,即$3x$人,男女生总人数为$60$人,可据此列出方程求解女生人数。
方程:$x + 3x = 60$
计算过程:
$4x = 60$
$x = 60÷4$
$x = 15$
答案:$x = 15$
五、解决问题。
淘气将4盒计算器包成一包。

1. 聪明的淘气想出了6种方案,第( )种包装法最省包装纸。

2. 至少需要多大面积的包装纸呢?
淘气将4盒计算器包成一包。

1. 聪明的淘气想出了6种方案,第( )种包装法最省包装纸。

2. 至少需要多大面积的包装纸呢?
答案:
解析:
本题考查了长方体的表面积计算以及如何通过组合减少表面积的知识点。
对于第一问,要想最省包装纸,那么就需要把计算器的最大面相粘合,从而使长方体表面积最小,通过观察可知,第③种包装法是把计算器最大的面($11×7$的面)相粘合,所以这种包装法最省包装纸。
对于第二问,先计算出按照第③种包装法组成的大长方体的长、宽、高,再根据长方体表面积公式$S=(ab + ah + bh) × 2$(其中$a$为长,$b$为宽,$h$为高)计算其表面积。
答案:
1. ③
2. 新长方体的长是$7×2 = 14$($\text{cm}$),宽是$11\text{cm}$,高是$2×2 = 4$($\text{cm}$)。
$(14×11 + 14×4 + 11×4) × 2$
$= (154 + 56 + 44) × 2$
$= (210 + 44) × 2$
$= 254×2$
$= 508$($\text{cm}^2$)
答:至少需要$508\text{cm}^2$的包装纸。
本题考查了长方体的表面积计算以及如何通过组合减少表面积的知识点。
对于第一问,要想最省包装纸,那么就需要把计算器的最大面相粘合,从而使长方体表面积最小,通过观察可知,第③种包装法是把计算器最大的面($11×7$的面)相粘合,所以这种包装法最省包装纸。
对于第二问,先计算出按照第③种包装法组成的大长方体的长、宽、高,再根据长方体表面积公式$S=(ab + ah + bh) × 2$(其中$a$为长,$b$为宽,$h$为高)计算其表面积。
答案:
1. ③
2. 新长方体的长是$7×2 = 14$($\text{cm}$),宽是$11\text{cm}$,高是$2×2 = 4$($\text{cm}$)。
$(14×11 + 14×4 + 11×4) × 2$
$= (154 + 56 + 44) × 2$
$= (210 + 44) × 2$
$= 254×2$
$= 508$($\text{cm}^2$)
答:至少需要$508\text{cm}^2$的包装纸。
$\frac {1}{1×2}+\frac {1}{2×3}= 1-\frac {1}{2}+\frac {1}{2}-\frac {1}{3}= \frac {2}{3}$
$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}= 1-\frac {1}{2}+\frac {1}{2}-\frac {1}{3}+\frac {1}{3}-\frac {1}{4}= 1-\frac {1}{4}= \frac {3}{4}$
$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}+\frac {1}{4×5}+\frac {1}{5×6}= ?$
$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}= 1-\frac {1}{2}+\frac {1}{2}-\frac {1}{3}+\frac {1}{3}-\frac {1}{4}= 1-\frac {1}{4}= \frac {3}{4}$
$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}+\frac {1}{4×5}+\frac {1}{5×6}= ?$
答案:
解析:
题目考查的是分数的裂项相消法,即一个分数可以表示为两个分数之差,通过这种方式可以将一系列分数的和简化为几个简单分数的运算。
观察给出的前两个式子,可以发现规律:对于形如$\frac{1}{n × (n+1)}$的分数,可以将其拆分为$\frac{1}{n} - \frac{1}{n+1}$。
应用这个规律到第三个式子,可以将每一项都拆分为两个分数之差,然后观察哪些分数可以相互抵消。
答案:
$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}+\frac {1}{4×5}+\frac {1}{5×6}$
$= 1-\frac {1}{2}+\frac {1}{2}-\frac {1}{3}+\frac {1}{3}-\frac {1}{4}+\frac {1}{4}-\frac {1}{5}+\frac {1}{5}-\frac {1}{6}$
$= 1-\frac {1}{6}$
$= \frac {5}{6}$
题目考查的是分数的裂项相消法,即一个分数可以表示为两个分数之差,通过这种方式可以将一系列分数的和简化为几个简单分数的运算。
观察给出的前两个式子,可以发现规律:对于形如$\frac{1}{n × (n+1)}$的分数,可以将其拆分为$\frac{1}{n} - \frac{1}{n+1}$。
应用这个规律到第三个式子,可以将每一项都拆分为两个分数之差,然后观察哪些分数可以相互抵消。
答案:
$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}+\frac {1}{4×5}+\frac {1}{5×6}$
$= 1-\frac {1}{2}+\frac {1}{2}-\frac {1}{3}+\frac {1}{3}-\frac {1}{4}+\frac {1}{4}-\frac {1}{5}+\frac {1}{5}-\frac {1}{6}$
$= 1-\frac {1}{6}$
$= \frac {5}{6}$
查看更多完整答案,请扫码查看


