《2025年实验班提优训练暑假衔接版三升四年级数学人教版》

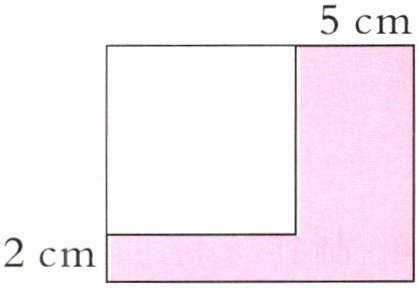
5. 新情境 助残接力 为了进一步弘扬“奉献、友爱、互助、进步”的志愿精神,某区开展小桔灯助残接力计划志愿服务活动。右下图是宣传栏的布局。已知涂色部分的面积是$66cm^{2}$,求图中白色正方形的面积。

答案：
$66-2×5=56(cm^{2})$
$56÷(5+2)=8(cm)$
$8×8=64(cm^{2})$
提示 利用分割法先把涂色部分分成三个小图形(如下图)。将涂色部分总面积减去C部分面积，即A和B部分的面积。A与B部分长相同可以拼成一个宽为$(2+5)cm$的长方形。再求出小长方形的长，也就是空白部分正方形的边长了。

6. 王爷爷家门前有一块长 31 米、宽 26 米的长方形菜地,为了便于浇水、施肥和捉虫,在菜地中修了两条宽都是 1 米的小路(如右下图),这样就把菜地分成了四块小菜地。这四块小菜地的面积和是多少平方米?

答案： $(31-1)×(26-1)=750$(平方米)

7. 如右下图,在长 30 米,宽 20 米的长方形绿地上有一条宽为 2 米的小路,求绿地的面积。

答案： $(30-2)×(20-2)=504$(平方厘米)
提示 利用平移法，可以得出一个新的长方形，再根据“(长-路宽)×(宽-路宽)=绿地面积”解题。

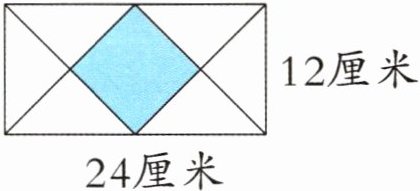
8. 如右下图,长方形长 24 厘米,宽 12 厘米,求涂色部分(正方形)的面积。

答案： $24×12=288$(平方厘米)
$288÷8×2=72$(平方厘米)

9. 用篱笆围成的一块长方形菜地如右下图,其中有一边是长为 25 米的墙壁,围成另外三条边的篱笆长是 55 米,这块长方形菜地的面积是多少平方米?

答案： $55-25=30$(米) $30÷2=15$(米)
$15×25=375$(平方米)

10. 学校利用“五一”假期将一块正方形荷花池进行扩建,把边长增加 4 米后,荷花池面积增加了 96 平方米(如图)。原来这个正方形荷花池的面积是多少平方米?

答案： $96-4×4=80$(平方米)
$80÷2=40$(平方米)
$40÷4=10$(米)
$10×10=100$(平方米)