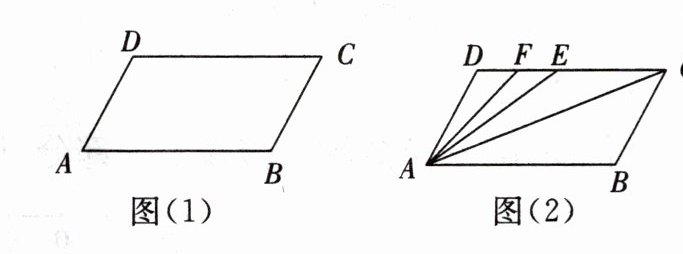
16. 如图(1)所示,已知$AD// BC,∠B= ∠D= 120^{\circ }$.
(1)请问:$AB与CD$平行吗?为什么?
(2)若点$E$,$F在线段CD$上,且满足$AC平分∠BAE$,$AF平分∠DAE$,如图(2)所示,求$∠FAC$的度数.
(3)若点$E在直线CD$上,且满足$∠EAC= \frac {1}{2}∠BAC$,求$∠ACD:∠AED$的值(请自己画出正确图形,并解答).
(1)请问:$AB与CD$平行吗?为什么?
(2)若点$E$,$F在线段CD$上,且满足$AC平分∠BAE$,$AF平分∠DAE$,如图(2)所示,求$∠FAC$的度数.
(3)若点$E在直线CD$上,且满足$∠EAC= \frac {1}{2}∠BAC$,求$∠ACD:∠AED$的值(请自己画出正确图形,并解答).

答案:
解:
(1)平行。
如题图
(1)所示,
∵AD//BC,
∴∠A+∠B=180°。
又
∵∠B=∠D=120°,
∴∠D+∠A=180°。
∴AB//CD。
(2)如题图
(2)所示,
∵AD//BC,∠B=∠D=120°,
∴∠DAB=60°。
∵AC 平分∠BAE,AF 平分∠DAE,
∴∠EAC=$\frac{1}{2}$∠BAE,∠EAF=$\frac{1}{2}$∠DAE。
∴∠FAC=∠EAC+∠EAF=$\frac{1}{2}$(∠BAE+∠DAE)=$\frac{1}{2}$∠DAB=30°。
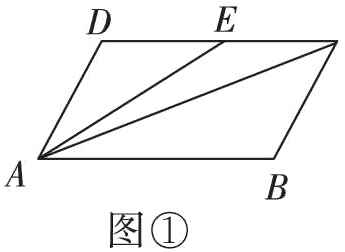
(3)①如图①所示,当点 E 在线段 CD 上时,
由
(1)可得 AB//CD,
∴∠ACD=∠BAC,∠AED=∠BAE。
又
∵∠EAC=$\frac{1}{2}$∠BAC,
∴∠ACD:∠AED=2:3。
②如图②所示,当点 E 在 DC 的延长线上时,
由
(1)可得 AB//CD,
∴∠ACD=∠BAC,∠AED=∠BAE。
又
∵∠EAC=$\frac{1}{2}$∠BAC,
∴∠ACD:∠AED=2:1。
③若点 E 在 CD 的延长线上时,∠EAC=$\frac{1}{2}$∠BAC 不成立,不符合题意。

解:
(1)平行。
如题图
(1)所示,
∵AD//BC,
∴∠A+∠B=180°。
又
∵∠B=∠D=120°,
∴∠D+∠A=180°。
∴AB//CD。
(2)如题图
(2)所示,
∵AD//BC,∠B=∠D=120°,
∴∠DAB=60°。
∵AC 平分∠BAE,AF 平分∠DAE,
∴∠EAC=$\frac{1}{2}$∠BAE,∠EAF=$\frac{1}{2}$∠DAE。
∴∠FAC=∠EAC+∠EAF=$\frac{1}{2}$(∠BAE+∠DAE)=$\frac{1}{2}$∠DAB=30°。
(3)①如图①所示,当点 E 在线段 CD 上时,
由
(1)可得 AB//CD,
∴∠ACD=∠BAC,∠AED=∠BAE。
又
∵∠EAC=$\frac{1}{2}$∠BAC,
∴∠ACD:∠AED=2:3。
②如图②所示,当点 E 在 DC 的延长线上时,
由
(1)可得 AB//CD,
∴∠ACD=∠BAC,∠AED=∠BAE。
又
∵∠EAC=$\frac{1}{2}$∠BAC,
∴∠ACD:∠AED=2:1。
③若点 E 在 CD 的延长线上时,∠EAC=$\frac{1}{2}$∠BAC 不成立,不符合题意。


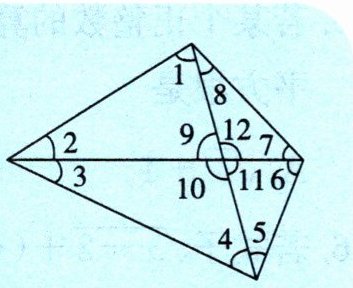
如图所示的是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角. 跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置$∠1跳到终点位置∠3$,写出其中两种不同路径,
路径1:$∠1\xrightarrow{同旁内角}∠9\xrightarrow{内错角}∠3$;
路径2:$∠1\xrightarrow{内错角}∠12\xrightarrow{内错角}∠6\xrightarrow{同位角}∠10\xrightarrow{同旁内角}∠3$.
试一试:(1)从起始角$∠1跳到终点角∠8$.
(2)从起始角$∠1$依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角$∠8$?
路径1:$∠1\xrightarrow{同旁内角}∠9\xrightarrow{内错角}∠3$;
路径2:$∠1\xrightarrow{内错角}∠12\xrightarrow{内错角}∠6\xrightarrow{同位角}∠10\xrightarrow{同旁内角}∠3$.
试一试:(1)从起始角$∠1跳到终点角∠8$.
(2)从起始角$∠1$依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角$∠8$?

答案:
解:
(1)路径:∠1$\xrightarrow{内错角}$∠12$\xrightarrow{同旁内角}$∠8。
(2)从起始角∠1 依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8。
路径:∠1$\xrightarrow{同位角}$∠10$\xrightarrow{内错角}$∠5$\xrightarrow{同旁内角}$∠8。
(1)路径:∠1$\xrightarrow{内错角}$∠12$\xrightarrow{同旁内角}$∠8。
(2)从起始角∠1 依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8。
路径:∠1$\xrightarrow{同位角}$∠10$\xrightarrow{内错角}$∠5$\xrightarrow{同旁内角}$∠8。
查看更多完整答案,请扫码查看


