2025年暑假作业与生活陕西人民教育出版社二年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业与生活陕西人民教育出版社二年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
下面图形哪些是轴对称图形,在对应的括号里画“√”
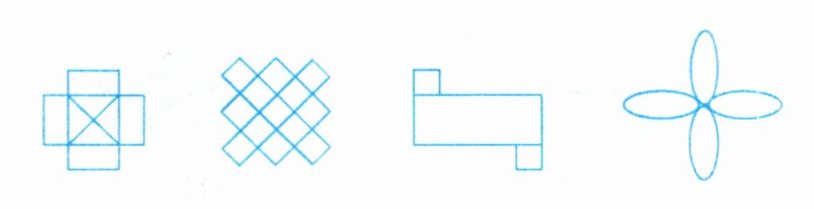
(

(
√
) (√
) () (√
)
答案:
(√) (√) ( ) (√)
1. 画出下图的轴对称图形。
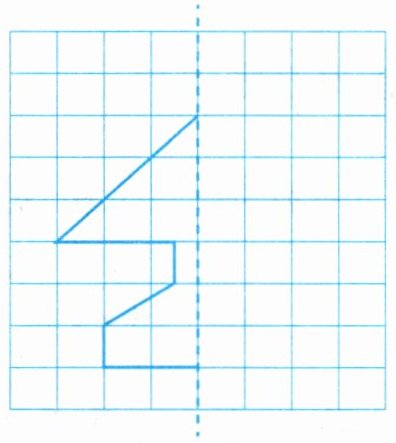

本题可根据轴对称图形的性质,通过找出已知图形各关键点关于对称轴的对称点,再依次连接对称点来画出轴对称图形。步骤一:确定已知图形的关键点。对于给定的图形,其关键点为图形的顶点。步骤二:找出各关键点关于对称轴的对称点。根据轴对称的性质:对称轴是对称点连线的垂直平分线,即对称点到对称轴的距离相等。对于图形上方的斜线段的两个顶点,分别测量它们到对称轴(图中虚线)的水平距离,然后在对称轴另一侧相同距离处确定对称点。对于下方阶梯状图形的各个顶点,同样测量它们到对称轴的水平距离,在对称轴另一侧确定对称点。步骤三:依次连接对称点。按照原图形中关键点的连接顺序,依次连接所找到的对称点,即可得到该图形的轴对称图形。(由于无法直接绘制图形,你可以根据上述步骤在给定的方格图中完成绘制。)
答案:
本题可根据轴对称图形的性质,通过找出已知图形各关键点关于对称轴的对称点,再依次连接对称点来画出轴对称图形。
步骤一:确定已知图形的关键点
对于给定的图形,其关键点为图形的顶点。
步骤二:找出各关键点关于对称轴的对称点
根据轴对称的性质:对称轴是对称点连线的垂直平分线,即对称点到对称轴的距离相等。
对于图形上方的斜线段的两个顶点,分别测量它们到对称轴(图中虚线)的水平距离,然后在对称轴另一侧相同距离处确定对称点。
对于下方阶梯状图形的各个顶点,同样测量它们到对称轴的水平距离,在对称轴另一侧确定对称点。
步骤三:依次连接对称点
按照原图形中关键点的连接顺序,依次连接所找到的对称点,即可得到该图形的轴对称图形。
(由于无法直接绘制图形,你可以根据上述步骤在给定的方格图中完成绘制。)
步骤一:确定已知图形的关键点
对于给定的图形,其关键点为图形的顶点。
步骤二:找出各关键点关于对称轴的对称点
根据轴对称的性质:对称轴是对称点连线的垂直平分线,即对称点到对称轴的距离相等。
对于图形上方的斜线段的两个顶点,分别测量它们到对称轴(图中虚线)的水平距离,然后在对称轴另一侧相同距离处确定对称点。
对于下方阶梯状图形的各个顶点,同样测量它们到对称轴的水平距离,在对称轴另一侧确定对称点。
步骤三:依次连接对称点
按照原图形中关键点的连接顺序,依次连接所找到的对称点,即可得到该图形的轴对称图形。
(由于无法直接绘制图形,你可以根据上述步骤在给定的方格图中完成绘制。)
2. 把下面的图形向左平移7格。
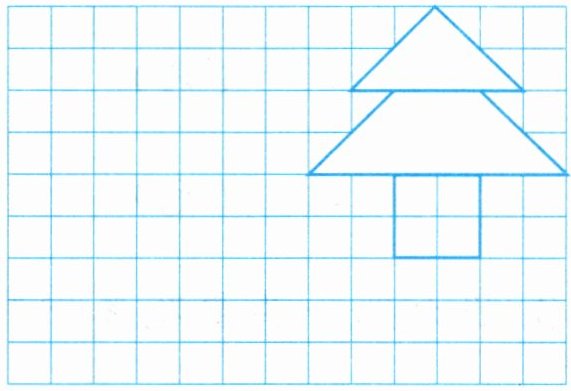

本题可根据平移的性质,通过确定图形关键点平移后的位置,进而得到平移后的图形。步骤一:确定图形的关键点。对于该组合图形(由三角形、梯形和正方形组成),分别找出每个图形的关键点,例如三角形的三个顶点、梯形的四个顶点、正方形的四个顶点。步骤二:将关键点向左平移7格。根据平移的规则,在平面直角坐标系中,向左平移n格,横坐标减n,纵坐标不变。在方格纸中,每一格代表一个单位长度,所以将每个关键点向左移动7格。步骤三:连接平移后的关键点。按照原图形中关键点的连接顺序,依次连接平移后的关键点,即可得到向左平移7格后的图形。(由于无法直接绘制图形,你可以根据上述步骤在给定的方格纸上进行绘制)综上,按照上述方法可完成图形向左平移7格的操作。
答案:
本题可根据平移的性质,通过确定图形关键点平移后的位置,进而得到平移后的图形。
步骤一:确定图形的关键点
对于该组合图形(由三角形、梯形和正方形组成),分别找出每个图形的关键点,例如三角形的三个顶点、梯形的四个顶点、正方形的四个顶点。
步骤二:将关键点向左平移$7$格
根据平移的规则,在平面直角坐标系中,向左平移$n$格,横坐标减$n$,纵坐标不变。在方格纸中,每一格代表一个单位长度,所以将每个关键点向左移动$7$格。
步骤三:连接平移后的关键点
按照原图形中关键点的连接顺序,依次连接平移后的关键点,即可得到向左平移$7$格后的图形。
(由于无法直接绘制图形,你可以根据上述步骤在给定的方格纸上进行绘制)
综上,按照上述方法可完成图形向左平移$7$格的操作。
步骤一:确定图形的关键点
对于该组合图形(由三角形、梯形和正方形组成),分别找出每个图形的关键点,例如三角形的三个顶点、梯形的四个顶点、正方形的四个顶点。
步骤二:将关键点向左平移$7$格
根据平移的规则,在平面直角坐标系中,向左平移$n$格,横坐标减$n$,纵坐标不变。在方格纸中,每一格代表一个单位长度,所以将每个关键点向左移动$7$格。
步骤三:连接平移后的关键点
按照原图形中关键点的连接顺序,依次连接平移后的关键点,即可得到向左平移$7$格后的图形。
(由于无法直接绘制图形,你可以根据上述步骤在给定的方格纸上进行绘制)
综上,按照上述方法可完成图形向左平移$7$格的操作。
填一填
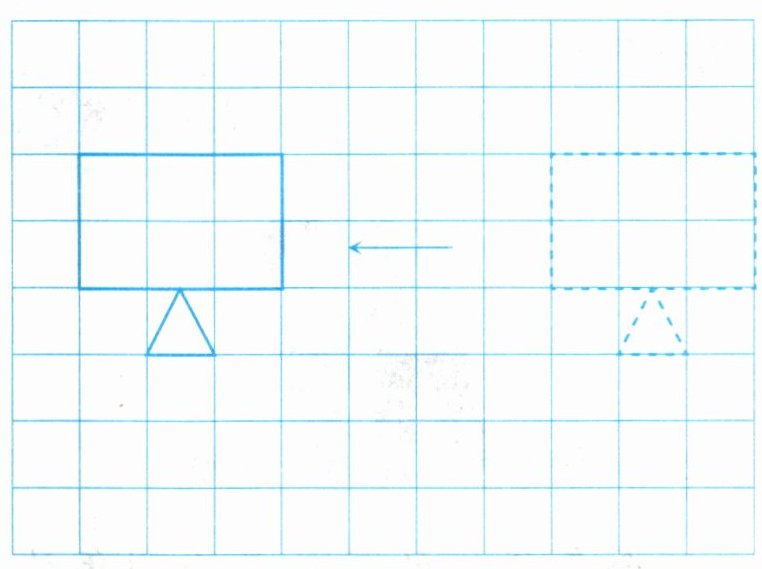
 向()平移了(
向()平移了(

 向()平移了(
向()平移了(

 向()平移了(
向()平移了(7
)格;
 向()平移了(
向()平移了(5
)格。
答案:
左 7 上 5
请你设计几个轴对称图形


以下是几个轴对称图形的设计(在方格纸上示意):
1. 等腰三角形:在方格纸上,先画底边(比如占 4 个方格长度),然后找到底边中点,从底边中点向上画高(比如占 3 个方格长度),连接顶点和底边两端点,得到等腰三角形,它关于底边上的高所在直线对称。
2. 矩形:画一个长占 5 个方格,宽占 3 个方格的矩形,它关于两组对边中点连线所在直线对称。
3. 菱形:先画两条互相垂直且平分的对角线(比如一条对角线占 4 个方格长度,另一条占 3 个方格长度),然后连接对角线的四个端点,得到菱形,它关于两条对角线所在直线对称。
1. 等腰三角形:在方格纸上,先画底边(比如占 4 个方格长度),然后找到底边中点,从底边中点向上画高(比如占 3 个方格长度),连接顶点和底边两端点,得到等腰三角形,它关于底边上的高所在直线对称。
2. 矩形:画一个长占 5 个方格,宽占 3 个方格的矩形,它关于两组对边中点连线所在直线对称。
3. 菱形:先画两条互相垂直且平分的对角线(比如一条对角线占 4 个方格长度,另一条占 3 个方格长度),然后连接对角线的四个端点,得到菱形,它关于两条对角线所在直线对称。
答案:
以下是几个轴对称图形的设计(在方格纸上示意):
1. 等腰三角形:在方格纸上,先画底边(比如占 4 个方格长度),然后找到底边中点,从底边中点向上画高(比如占 3 个方格长度),连接顶点和底边两端点,得到等腰三角形,它关于底边上的高所在直线对称。
2. 矩形:画一个长占 5 个方格,宽占 3 个方格的矩形,它关于两组对边中点连线所在直线对称。
3. 菱形:先画两条互相垂直且平分的对角线(比如一条对角线占 4 个方格长度,另一条占 3 个方格长度),然后连接对角线的四个端点,得到菱形,它关于两条对角线所在直线对称。
1. 等腰三角形:在方格纸上,先画底边(比如占 4 个方格长度),然后找到底边中点,从底边中点向上画高(比如占 3 个方格长度),连接顶点和底边两端点,得到等腰三角形,它关于底边上的高所在直线对称。
2. 矩形:画一个长占 5 个方格,宽占 3 个方格的矩形,它关于两组对边中点连线所在直线对称。
3. 菱形:先画两条互相垂直且平分的对角线(比如一条对角线占 4 个方格长度,另一条占 3 个方格长度),然后连接对角线的四个端点,得到菱形,它关于两条对角线所在直线对称。
查看更多完整答案,请扫码查看


