《2025年优秀生快乐假期每一天全新暑假作业本八年级数学人教版》

2. 如图,在正方形ABCD中,E为AB上一点,F为BC上一点. 若$AE+CF= EF$,求$∠EDF$的度数.

答案： 提示:延长 EA 至 H,使 AH=CF,连接 DH,$\triangle DAH\cong\triangle DCF$,$\angle FDC=\angle HDA$,DH=DF,再证$\triangle DHE\cong\triangle DFE$,得$\angle HDE=\angle EDF$,$\therefore\angle HDA+\angle ADE=\angle EDF$,$\angle ADE+\angle FDC=\angle EDF$,$\angle ADE+\angle FDC+\angle EDF=90^\circ$,$\therefore 2\angle EDF=90^\circ$,$\angle EDF=45^\circ$.

四、如图,P为$□ ABDC$内任意一点,$△PAB面积为S_{1},△PCD面积为S_{2},□ ABDC$面积为S.

(1)$S_{1}$、$S_{2}$与S的关系如何? 请证明.
(2)若点P在$□ ABDC$外部(P在边CD下方),$S_{1}$、$S_{2}$与S的关系又如何?

答案：
(1)$S_1+S_2=\frac{S}{2}$ 证明:过 P 点分别作AB、CD 的垂线,PE⊥AB,PF⊥CD,$S_{\triangle PAB}=\frac{1}{2}× PE\cdot AB$,$S_{\triangle PDC}=\frac{1}{2}PF\cdot CD$.$S_1+S_2=\frac{1}{2}AB(PE+PF)$,而 PE+PF 等于□ABDC 中 AB 边上的高,$\therefore S_1+S_2=\frac{1}{2}S$.
(2)$S_1-S_2=\frac{S}{2}$

(四川绵阳最新中考题)如图,$□ ABCD$的对角线AC,BD相交于点O,点E,F在AC上,且$AE= CF.$

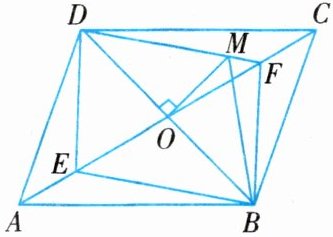
(1)求证:$BE// DF;$
(2)过点O作$OM⊥BD$,垂足为O,交DF于点M,若$△BFM$的周长为12,求四边形BEDF的周长.

答案：
(1)证明:
∵四边形 ABCD 是平行四边形,$\therefore AB// DC$,AB=DC,$\therefore\angle BAE=\angle DCF$,在$\triangle ABE$与$\triangle CDF$中,$\left\{\begin{array}{l} AB=CD\\ \angle BAE=\angle DCF,\\ AE=CF\end{array}\right.$$\therefore\triangle ABE\cong\triangle CDF(SAS)$,$\therefore\angle AEB=\angle CFD$,$\therefore\angle BEF=\angle DFE$,$\therefore BE// DF$;
(2)解:由
(1)知,$\triangle ABE\cong\triangle CDF$,BE$//$DF,$\therefore BE=DF$,$\therefore$四边形 BEDF 是平行四边形,$\therefore DO=BO$,
∵OM⊥BD,$\therefore DM=BM$,
∵$\triangle BFM$的周长为 12,$\therefore BM+MF+BF=DM+MF+BF=DF+BF=12$,$\therefore BF+DF+BE+DE=2(BF+DF)=2×12=24$.$\therefore$四边形 BEDF 的周长为 24.