《2025年通城学典课时作业本四年级数学上册苏教版江苏专版》

1. 把下面的算式合并成综合算式。
(1)$30 - 10 = 20$ $40×20 = 800$
$800÷16 = 50$
综合算式：($40×(30−10)÷16 = 50$)
(2)$96÷6 = 16$ $16 + 74 = 90$
$18×90 = 1620$
综合算式：($18×(96÷6 + 74)=1620$)
(3)$132 + 129 = 261$ $368 - 261 = 107$
$107×5 = 535$
综合算式：($[368−(132 + 129)]×5 = 535$)
(4)$570÷19 = 30$ $270÷30 = 9$
$810÷9 = 90$
综合算式：($810÷[270÷(570÷19)] = 90$)

答案： 1.
(1) $40×(30−10)÷16 = 50$
(2) $18×(96÷6 + 74) = 1620$
(3) $[368−(132 + 129)]×5 = 535$
(4) $810÷[270÷(570÷19)] = 90$

(1)要使算式“$43 + 22×5 - 3$”按照“先减、再乘、最后加”的顺序运算,应该怎么添加括号？正确的是(A)。
A.$43 + 22×(5 - 3)$
B.$(43 + 22×5) - 3$
C.$(43 + 22)×(5 - 3)$

答案： A

(2)下面算式中的括号去掉后,计算结果不变的是(B)。
A.$(480 + 20)×4$
B.$48×(20÷4)$
C.$480÷(20×4)$

答案： B

3. 根据运算顺序添上括号,并计算结果。
(1)先算乘法,再算减法,最后算加法。
$875 + 29 - 9×3 = $$875+(29−9×3) = 877$
(2)先算加法,再算减法,最后算乘法。
$875 + 29 - 9×3 = $$(875 + 29−9)×3 = 2685$
(3)先算减法,再算乘法,最后算加法。
$875 + 29 - 9×3 = $$875+(29−9)×3 = 935$

答案： 3.
(1) $875+(29−9×3) = 877$
(2) $(875 + 29−9)×3 = 2685$
(3) $875+(29−9)×3 = 935$

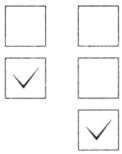
4.(创新应用)在每组得数大的算式后面的$□$里画“√”。
$\begin{cases}80 - (750÷25 + 5) □ \\80 - 750÷25 + 5 □ \end{cases} $
$\begin{cases}16×(70 - 50 + 34) □ \\16×(70 - 50) + 34 □ \\16×70 - (50 + 34) □ \end{cases} $

答案：
4.
　

5.(思维过程)在算式$450÷30 + 4×15$中,怎样添加小括号使所得的结果最大？怎样添加小括号使所得的结果最小？请算出最大的结果和最小的结果。

答案： 5.结果最大:$(450÷30 + 4)×15 = 285$
结果最小:$450÷(30 + 4×15) = 5$
解析:观察后发现算式中有除法、加法和乘法，要使结果最大，最后应算乘法;要使结果最小，最后应算除法。