《2025年通城学典课时作业本六年级数学上册苏教版江苏专版》

(1) 一个正方体的棱长总和是 48 cm,它的表面积是( )$cm^{2}$,体积是( )$cm^{3}$。

答案： 96 64

(2) 一个长方体木块长 16 cm,宽 10 cm,高8 cm,从这个木块上切下一个最大的正方体后,剩下部分的体积是( )$cm^{3}$。

答案： 768

(3) (易错题)一根长 0.8 米的长方体木料的横截面是正方形,把它沿与横截面平行的方向锯成两段,表面积比原来增加了32 平方厘米。原来这根长方体木料的体积是( )立方厘米。

答案： 1280 易错分析:把长方体木料沿与横截面平行的方向锯成两段,表面积增加的是 2 个横截面的面积。

2. 如图所示为一个长方体形状的孔明灯,它的下面是边长为 30 cm 的正方形,高为 50 cm。
(1) 除下面外,它的其他面都要糊上阻燃纸,制作这个孔明灯至少需要多少平方厘米的阻燃纸?

(2) 这个孔明灯的体积是多少立方厘米?
(3) 制作一个这样的孔明灯框架需要的材料有 50 cm 的长竹条 4 根和 30 cm 的短竹条8 根。王叔叔现在有长竹条 20 根和短竹条35 根,王叔叔想用这些材料制作 5 个这样的孔明灯框架,你觉得够吗?

答案：
(1) $ 30×30+30×50×4=6900(cm^{2}) $
(2) $ 30×30×50=45000(cm^{3}) $
(3) 制作一个孔明灯框架需要长竹条 4 根和短竹条 8 根,制作 5 个这样的孔明灯框架就需要长竹条 $ 4×5=20 $ (根),短竹条 $ 8×5=40 $ (根) $ 40＞35 $ 不够制作 5 个这样的孔明灯框架

3. (南京真题)一个花坛(如图)从外面量高0.5 米,底面是边长为 1.2 米的正方形。四周用砖头砌成,厚度是 0.2 米,中间填满泥土。
(1) 这个花坛所占的空间有多大?

(2) 花坛里的泥土有多少立方米?
(3) 若在花坛的四周贴上瓷砖,则贴瓷砖的面积是多少平方米?

答案：
(1) $ 1.2×1.2×0.5=0.72 $ (立方米)
(2) $ (1.2-0.2×2)×(1.2-0.2×2)×0.5=0.32 $ (立方米)
(3) $ 1.2×0.5×4=2.4 $ (平方米)

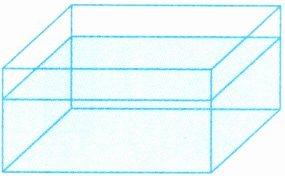
4. 一个完全封闭的长方体玻璃容器,从里面量,长 20 厘米,宽 16 厘米,高 10 厘米,平放时水面高 7 厘米。如果把这个容器竖起来放(右面为底面),那么水面高多少厘米?

答案： $ 20×16×7=2240 $ (立方厘米) $ 2240÷16÷10=14 $ (厘米)

5. (南通真题)看图回答问题。(下图是用棱长为1厘米的小正方体拼成的)
(1) 拼成这个图形一共用了( )个这样的小正方体。
(2) 拼成图形的表面积是( )平方厘米。
(3) 不移动原有的小正方体,至少要添加( )个这样的小正方体,才能拼成一个大正方体。

答案：
(1) 20 解析:根据题意,数小正方体可以从上往下一层一层地数,下一层被遮住的数量与上一层的总数量相同:第 1 层 1 个,第 2 层 3 个(露出的 2 个和被遮住的 1 个),第 3 层 6 个(露出的 3 个和被遮住的 3 个),第 4 层 10 个(露出的 4 个和被遮住的 6 个),把每层个数相加即可。
(2) 60 解析:从上面和下面观察,都能看到 10 个小正方形;从左面和右面观察,都能看到 10 个小正方形;从前面和后面观察,都能看到 10 个小正方形。所以无论从哪一个面观察,都能看到 10 个小正方形,即这个立体图形的表面积等于 $ 10×6 $ 个小正方形的面积。先利用正方形的面积公式求出其中一个小正方形的面积,再乘小正方形的数量,即可求出该立体图形的表面积。
(3) 44 解析:观察题图,可得拼成的大正方体每条棱上至少有 4 个小正方体,即至少一共需要 $ 4×4×4=64 $ (个)小正方体。用 64 个小正方体减去已有的 20 个小正方体,即可得到至少要添加多少个这样的小正方体。