《2025年启东中学作业本八年级数学上册苏科版连淮专版》

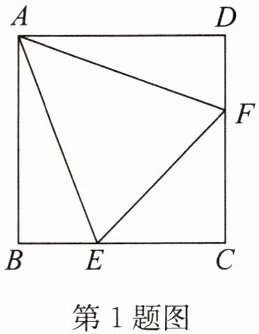
1. 如图,$E$,$F$分别是边长为1的正方形$ABCD的边BC$,$CD$上的点. 若$△ECF$的周长是2,则$∠EAF$的度数为( )


A.$40^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$

答案：
1.B　点拨:如答图，将△ADF绕点A顺时针旋转90°至△ABG的位置，则△ADF≌△ABG,
∴DF=BG,AG=AF,∠ABG=∠D=∠ABE=90°,∠DAF=∠BAG.
∴∠ABG+∠ABE=180°,
∴G,B,E三点共线.
∵正方形ABCD的边长为1,△ECF的周长是2,
∴EF+CE+CF=CF+DF+CE+BE=2,
∴EF=DF+BE=BE+BG=GE;又
∵AE=AE,
∴△AEF≌△AEG(SSS).
∴∠EAF=∠EAG;又
∵∠FAG=90°,
∴∠EAF=45°.故选B.

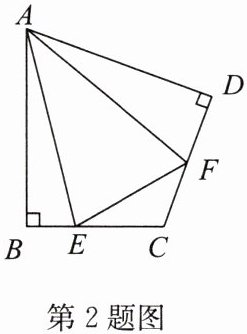
2. 如图,在四边形$ABCD$中,$AB = AD$,$∠B = ∠D = 90^{\circ}$,$E$,$F分别是边BC$,$CD$上的点,$∠EAF= \frac{1}{2}∠BAD$.
(1)求证：$EF = BE + FD$；
(2)求证：$FA平分∠DFE$.

答案：
2.证明:
(1)如答图,延长EB至点G,使BG=DF,连接AG.

在△ABG和△ADF中，{AB=AD,∠ABG=∠D=90°,BG=DF,
∴△ABG≌△ADF(SAS).
∴∠1=∠2,AF=AG;
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠2+∠3=$\frac{1}{2}$∠BAD=∠1+∠3=∠EAG.
∴∠EAF=∠EAG;又
∵AE=AE,
∴△AEG≌△AEF(SAS).
∴EF=EG,∠G=∠AFE;
∵EG=BE+BG=BE+DF,
∴EF=BE+FD.
(2)
∵△ABG≌△ADF,
∴∠G=∠AFD.又
∵∠G=∠AFE,
∴∠AFE=∠AFD.
∴FA平分∠DFE.