《2025年启东中学作业本八年级数学上册苏科版连淮专版》

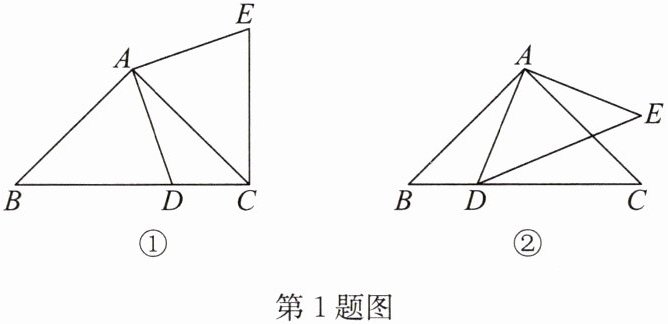
1. (1)如图①,在$Rt△ABC$中,$∠BAC= 90^{\circ },AB= AC$,D 为 BC 边上一点(不与点 B,C 重合),将线段 AD 绕点 A 逆时针旋转$90^{\circ }$得到线段 AE,连接 EC. 求证:$△ABD\cong △ACE;$
(2)如图②,在$Rt△ABC和Rt△ADE$中,$∠BAC= ∠DAE= 90^{\circ },AB= AC,AD= AE,将△ADE$绕点 A 旋转,使点 D 落在 BC 边上,试探索$AD^{2},BD^{2},CD^{2}$之间满足的数量关系,并证明你的结论.

答案： 1.
(1)证明:
∵∠BAC=∠DAE=90°,
∴∠BAC−∠DAC=∠DAE−∠DAC,
　即∠BAD=∠CAE.
　在△BAD和△CAE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE(SAS).
(2)解:2AD²=BD²+CD²,理由如下:连接EC;
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
　在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=45°,
　又
∵∠ACB=∠B=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,
∴DE²=CE²+CD².
　在Rt△ADE中,DE²=AD²+AE²=2AD²,
∴2AD²=BD²+CD².

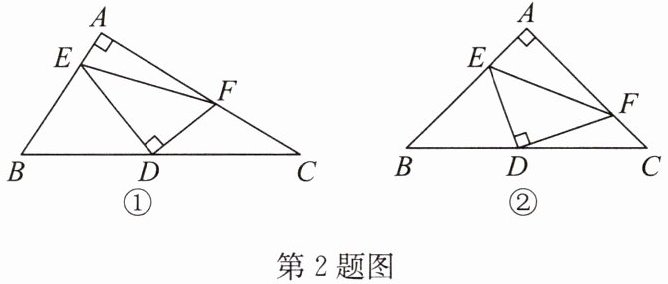
2. 在$Rt△ABC$中,$∠BAC= 90^{\circ }$,D 是斜边 BC 的中点,E,F 分别是 AB,AC 边上的点,且$DE⊥DF$,连接 EF.
(1)如图①,求证:$∠BED= ∠AFD;$
(2)如图①,求证:$BE^{2}+CF^{2}= EF^{2};$
(3)如图②,当$∠ABC= 45^{\circ }$时,若$BE= 12,CF= 5$,求$△DEF$的面积.

答案：
2.
(1)证明:
∵DE⊥DF,
∴∠EDF=90°.
∵∠BAC=90°,
∴∠AFD+∠AED=180°.
∵∠BED+∠AED=180°,
∴∠BED=∠AFD.
(2)证明:如答图①,延长ED到点P,使DP=DE,连接FP,CP.
　　　　　　　
　在△BED和△CPD中,ED=PD,∠EDB=∠PDC,BD=CD,
∴△BED≌△CPD(SAS).
∴BE=CP,∠B=∠PCD.
　在△EDF和△PDF中,DE=DP,∠EDF=∠PDF=90°,DF=DF,
∴△EDF≌△PDF(SAS).
∴EF=FP.
∵∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°.
　在Rt△FCP中,根据勾股定理,得CF²+CP²=PF²,
∵BE=CP,PF=EF,
∴BE²+CF²=EF².
(3)解:如答图②,连接AD.
　由题意知△ABC为等腰直角三角形.
∵D为BC边的中点,
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∴∠AFD+∠FDC=90°.
∵DE⊥DF,
∴∠EDA+∠ADF=90°,
∴∠EDA=∠FDC.
　在△AED和△CFD中,∠EAD=∠FCD,AD=CD,∠ADE=∠CDF,
∴△AED≌△CFD(ASA).
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴EF边上的高为$\frac{1}{2}$EF.
　由
(2)知EF²=BE²+CF²=144+25=169,
∴EF=13.
∴S△DEF=$\frac{1}{2}$·EF·$\frac{1}{2}$EF=$\frac{1}{4}$EF²=$\frac{169}{4}$,