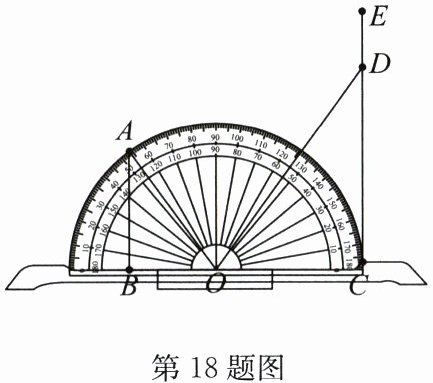
18.(8分)(2024·连云港期末)小丽在物理实验课上利用如图所示的“光的反射演示器”直观呈现了光的反射原理。她用激光笔从量角器左边边缘点$A$处发出光线,经量角器圆心$O$处(此处放置平面镜)反射后,反射光线落在右边光屏$CE上的点D$处(点$C$也在量角器的边缘上,$O$为量角器的中心,$C$,$O$,$B$三点共线,$AB\perp BC$,$CE\perp BC$)。小丽在实验中还记录下了$AB = 6cm$,$BC = 12cm$。依据记录的数据,求量角器的半径$OC$的长。

答案:
解:设量角器的半径OC的长为x cm,则OB=(12 - x),OA=x cm.
∵AB⊥BC,
∴AB²+BO²=OA².
∵AB=6 cm,
∴6²+(12 - x)²=x²,解得x=7.5.
∴量角器的半径OC的长为7.5 cm.
∵AB⊥BC,
∴AB²+BO²=OA².
∵AB=6 cm,
∴6²+(12 - x)²=x²,解得x=7.5.
∴量角器的半径OC的长为7.5 cm.
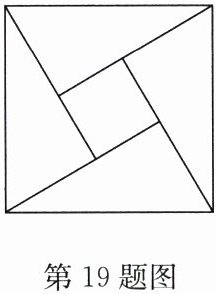
19.(8分)(2024·赣榆区期中)古代数学家赵爽创建了一幅“弦图”,如图所示,该“弦图”由四个完全相同的直角三角形拼在一起得到一个大正方形和一个小正方形。已知直角三角形的两条直角边长分别为$a$,$b(a>b)$。
(1)请你直接写出大正方形的面积;(用含$a$,$b$的代数式表示)
(2)若$(a + b)^{2}= 26$,大正方形的面积为17,求小正方形的面积。
(1)请你直接写出大正方形的面积;(用含$a$,$b$的代数式表示)
(2)若$(a + b)^{2}= 26$,大正方形的面积为17,求小正方形的面积。

答案:
解:
(1)
∵大正方形的面积为直角三角形斜边的平方,
∴大正方形的面积为a²+b².
(2)由
(1),知a²+b²=17,①又(a + b)²=26,即a²+b²+2ab=26,②② - ①,得2ab=9,
∴(a - b)²=a²+b² - 2ab=17 - 9=8,
∴小正方形的面积为8.
(1)
∵大正方形的面积为直角三角形斜边的平方,
∴大正方形的面积为a²+b².
(2)由
(1),知a²+b²=17,①又(a + b)²=26,即a²+b²+2ab=26,②② - ①,得2ab=9,
∴(a - b)²=a²+b² - 2ab=17 - 9=8,
∴小正方形的面积为8.
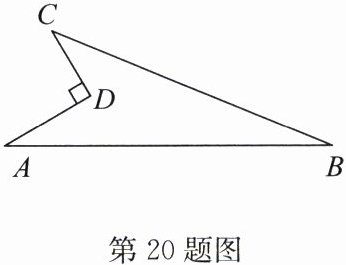
20.(8分)(2024·宿迁共同体期末)如图是一块地的示意图,已知$AD = 8cm$,$CD = 6cm$,$\angle D = 90^{\circ}$,$AB = 26cm$,$BC = 24cm$,求这块地的面积。

答案:
解:如答图,连接AC.
∵AD=8 cm,CD=6 cm,∠D=90°,
∴AC=√(6² + 8²)=10(cm).
∵AB=26 cm,BC=24 cm,10²+24²=26²,即AC²+BC²=AB²,
∴△ABC为直角三角形,∠ACB=90°,
∴S四边形ABCD=S△ABC - S△ACD=1/2×10×24 - 1/2×6×8=96(cm²).
解:如答图,连接AC.
∵AD=8 cm,CD=6 cm,∠D=90°,
∴AC=√(6² + 8²)=10(cm).
∵AB=26 cm,BC=24 cm,10²+24²=26²,即AC²+BC²=AB²,
∴△ABC为直角三角形,∠ACB=90°,
∴S四边形ABCD=S△ABC - S△ACD=1/2×10×24 - 1/2×6×8=96(cm²).

查看更多完整答案,请扫码查看


