9. 一个三角形的三边长分别为3,4,5,那么最长边上的高等于
2.4
。
答案:
2.4
10. 木工师傅要做一张长方形的桌面。完成后,量得桌面的长为100cm,宽为80cm,对角线为130cm,则做出的这个桌面
不合格
。(填“合格”或“不合格”)
答案:
不合格
11. 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”。如图,设勾$a = 6$,弦$c = 10$,则小正方形$ABCD$的面积是
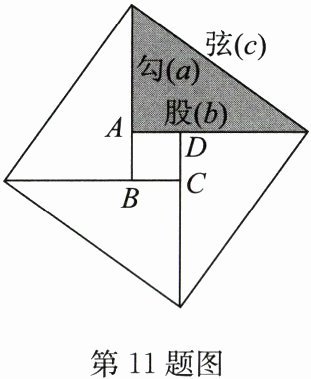
4
。
答案:
4
12. 在$\triangle ABC$中,$AD$是高,$AD = 6$,$CD = 1$,若$\triangle ABC$的面积为12,则线段$BD$的长度为
3或5
。
答案:
3或5
13. 如图,在$\triangle ABC$中,$AB = 5$,$AC = 13$,$BC边上的中线AD = 6$,则$\triangle ABD$的面积是
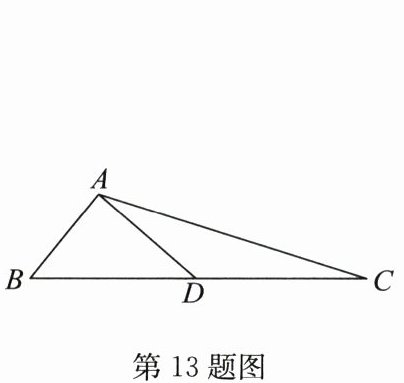
15
。
答案:
15
14. 我国明代一位杰出的数学家提出一道“荡秋千”的数学问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”其意思为:如图所示,当秋千静止在地面上时,秋千的踏板离地的距离为一尺$(CE = 1尺)$,将秋千的踏板往前推两步(每一步合五尺,即$EF = 10$尺),秋千的踏板与人一样高,这个人的身高为五尺$(DF = 5尺)$,则秋千的绳索$AC$的长度是______尺。
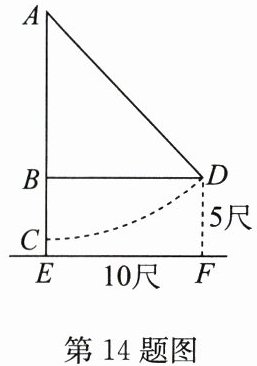

14.5
答案:
14.5
15. 如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点$B$处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的$A$处,则蚂蚁从外壁$A处到内壁B$处的最短距离为______cm。(杯壁厚度不计)
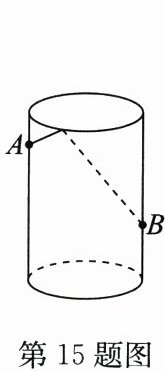

20
答案:
20
16. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AB = 5$,$BC = 3$,$P是AB$边上的动点(不与点$B$重合),将$\triangle BCP沿CP$所在的直线翻折,得到$\triangle B'CP$,连接$B'A$,则$B'A$长度的最小值是______
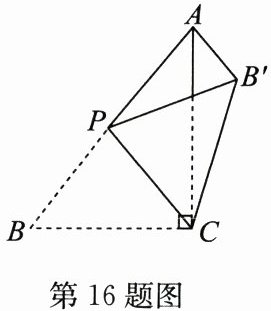
1
。
答案:
1
17.(6分)如图,在$\triangle ABC$中,$AD\perp BC于点D$,$AB = 5$,$BD = 3$,$DC = 6$。
求:(1)$AD$的长;
(2)$\triangle ABC$的面积。
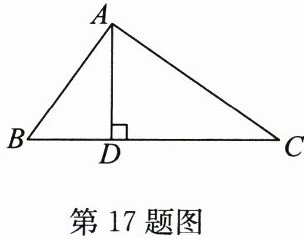
求:(1)$AD$的长;
(2)$\triangle ABC$的面积。

答案:
1. (1)
解:在$Rt\triangle ABD$中,根据勾股定理$AB^{2}=AD^{2}+BD^{2}$,已知$AB = 5$,$BD = 3$,设$AD$的长为$x$,则$x=\sqrt{AB^{2}-BD^{2}}$。
把$AB = 5$,$BD = 3$代入可得:$AD=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4$。
2. (2)
解:因为$BC=BD + DC$,$BD = 3$,$DC = 6$,所以$BC=3 + 6=9$。
又因为$AD\perp BC$,$AD = 4$,根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}× BC× AD$。
把$BC = 9$,$AD = 4$代入可得:$S_{\triangle ABC}=\frac{1}{2}×9×4 = 18$。
综上,(1)$AD$的长为$4$;(2)$\triangle ABC$的面积为$18$。
解:在$Rt\triangle ABD$中,根据勾股定理$AB^{2}=AD^{2}+BD^{2}$,已知$AB = 5$,$BD = 3$,设$AD$的长为$x$,则$x=\sqrt{AB^{2}-BD^{2}}$。
把$AB = 5$,$BD = 3$代入可得:$AD=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4$。
2. (2)
解:因为$BC=BD + DC$,$BD = 3$,$DC = 6$,所以$BC=3 + 6=9$。
又因为$AD\perp BC$,$AD = 4$,根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}× BC× AD$。
把$BC = 9$,$AD = 4$代入可得:$S_{\triangle ABC}=\frac{1}{2}×9×4 = 18$。
综上,(1)$AD$的长为$4$;(2)$\triangle ABC$的面积为$18$。
查看更多完整答案,请扫码查看


