20.(8分)(2024·宿城期末)如图,MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为12,求BC的长;
(2)∠BAC= 105°,求∠PAQ的度数.
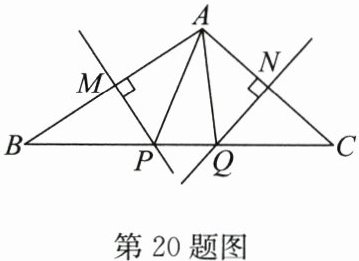
(1)若△APQ的周长为12,求BC的长;
(2)∠BAC= 105°,求∠PAQ的度数.

答案:
(1)
∵MP和NQ分别垂直平分AB和AC,
∴AP=BP,AQ=CQ,
∴△APQ的周长为AP + PQ + AQ = BP + PQ + CQ = BC.
∵△APQ的周长为12,
∴BC=12.
(2)
∵AP=BP,AQ=CQ,
∴∠B=∠BAP,∠C=∠CAQ.
∵∠BAC=105°,
∴∠BAP+∠CAQ=∠B+∠C=180° - ∠BAC=180° - 105° = 75°,
∴∠PAQ=∠BAC - (∠BAP+∠CAQ)=105° - 75° = 30°.
(1)
∵MP和NQ分别垂直平分AB和AC,
∴AP=BP,AQ=CQ,
∴△APQ的周长为AP + PQ + AQ = BP + PQ + CQ = BC.
∵△APQ的周长为12,
∴BC=12.
(2)
∵AP=BP,AQ=CQ,
∴∠B=∠BAP,∠C=∠CAQ.
∵∠BAC=105°,
∴∠BAP+∠CAQ=∠B+∠C=180° - ∠BAC=180° - 105° = 75°,
∴∠PAQ=∠BAC - (∠BAP+∠CAQ)=105° - 75° = 30°.
21.(10分)如图,在△ADB中,∠ADB= 60°,DC平分∠ADB,交AB于点C,且DC⊥AB,过点C作CE//DA交DB于点E,连接AE.
求证:(1)△ADB是等边三角形;(2)AE⊥DB.
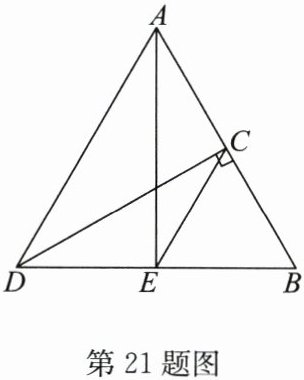
求证:(1)△ADB是等边三角形;(2)AE⊥DB.

答案:
(1)证明:
∵∠ADB=60°,DC平分∠ADB,
∴∠ADC=∠BDC=30°.
∵DC⊥AB,
∴∠DCB=∠DCA=90°,
∴∠B=∠DAC=90° - 30° = 60°,
∴∠ADB=∠B=∠DAB=60°,
∴△ADB是等边三角形.
(2)
∵CE//DA,
∴∠BEC=∠ADB=60°,
∴∠CEB=∠CBE=∠ECB=60°,
∴△CEB是等边三角形,
∴CE=BE=CB.
∵∠BDC=30°,∠DCB=90°,
∴BC=1/2BD,
∴CE=1/2BD,
∴E是BD的中点,
∴AE是边BD的中线.
∵△ADB是等边三角形,
∴AE⊥BD.
(1)证明:
∵∠ADB=60°,DC平分∠ADB,
∴∠ADC=∠BDC=30°.
∵DC⊥AB,
∴∠DCB=∠DCA=90°,
∴∠B=∠DAC=90° - 30° = 60°,
∴∠ADB=∠B=∠DAB=60°,
∴△ADB是等边三角形.
(2)
∵CE//DA,
∴∠BEC=∠ADB=60°,
∴∠CEB=∠CBE=∠ECB=60°,
∴△CEB是等边三角形,
∴CE=BE=CB.
∵∠BDC=30°,∠DCB=90°,
∴BC=1/2BD,
∴CE=1/2BD,
∴E是BD的中点,
∴AE是边BD的中线.
∵△ADB是等边三角形,
∴AE⊥BD.
22.(10分)(2024·赣榆区期中)【模型建立】(1)如图①,在Rt△ABC与Rt△ADE中,AB= AC,AD= AE,∠BAC= ∠DAE= 90°,求证:△AEC≌△ADB.
【模型应用】(2)如图②,在△ABC与△ADE中,AB= AC,AD= AE,∠BAC= ∠DAE= 90°,B,D,E三点在一条直线上,AC与BE交于点F,且F为AC的中点.
①求∠BEC的度数;
②若CE= 3,求△AEF的面积.
【拓展提高】(3)如图③,在△ABC与△ADE中,AB= AC,DA= DE,∠BAC= ∠ADE= 90°,AC与BE交于点F,DC= DF,CD⊥DF,△BCF的面积为18,求AF的长.
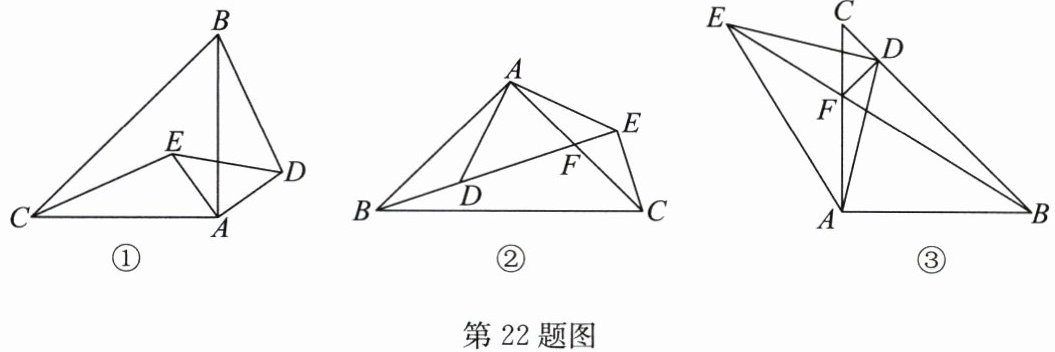
【模型应用】(2)如图②,在△ABC与△ADE中,AB= AC,AD= AE,∠BAC= ∠DAE= 90°,B,D,E三点在一条直线上,AC与BE交于点F,且F为AC的中点.
①求∠BEC的度数;
②若CE= 3,求△AEF的面积.
【拓展提高】(3)如图③,在△ABC与△ADE中,AB= AC,DA= DE,∠BAC= ∠ADE= 90°,AC与BE交于点F,DC= DF,CD⊥DF,△BCF的面积为18,求AF的长.

答案:
(1)证明:
∵∠BAC=∠DAE,
∴∠EAC=∠DAB.在△AEC和△ADB中,AC=AB,∠EAC=∠DAB,AE=AD,
∴△AEC≌△ADB(SAS).
(2)解:①
∵∠BAC=∠DAE,
∴∠EAC=∠DAB.在△AEC和△ADB中,AC=AB,∠EAC=∠DAB,AE=AD,
∴△AEC≌△ADB(SAS),
∴∠ABE=∠ACE,
∴∠BEC=180° - ∠ACE - ∠EAC - ∠AEB=180° - ∠ABE - ∠EAC - ∠AEB=∠BAC=90°. ②作AG⊥BE于点G,如答图①所示.
∵△AEC≌△ADB,
∴BD=EC=3.
∵F为AC的中点,
∴AF=CF.在△AGF和△CEF中,∠AFG=∠CFE,∠AGF=∠CEF,AF=CF,
∴△AGF≌△CEF(AAS),
∴AG=EC=3,
∴S△ACE=S△ADB=1/2×3×3 = 4.5.
∵F为AC的中点,
∴S△AEF=1/2S△ACE=1/2×4.5 = 2.25.
(3)解:连接EC,如答图②所示.
∵∠BAC=∠ADE=90°,CD⊥DF,
∴∠CDE=∠FDA.在△CDE和△FDA中,CD=FD,∠CDE=∠FDA,DE=DA,
∴△CDE≌△FDA(SAS),
∴CE=AF,∠DCE=∠AFD.
∵DC=DF,CD⊥DF,
∴△CDF为等腰直角三角形,
∴∠DCF=∠CFD=45°,
∴∠AFD=180° - 45° = 135°,
∴∠DCE=∠AFD=135°,
∴∠ECA=135° - 45° = 90°,
∴∠ACE=∠BAC=90°,
∴CE//AB,
∴S△ACE=S△FCB.
∵△CEF是公共部分,
∴S△AEF=S△CFB=18.设AF的长度为a,则S△AEF=a²/2 = 18,解得a = 6(负值已舍去),故AF的长为6.
(1)证明:
∵∠BAC=∠DAE,
∴∠EAC=∠DAB.在△AEC和△ADB中,AC=AB,∠EAC=∠DAB,AE=AD,
∴△AEC≌△ADB(SAS).
(2)解:①
∵∠BAC=∠DAE,
∴∠EAC=∠DAB.在△AEC和△ADB中,AC=AB,∠EAC=∠DAB,AE=AD,
∴△AEC≌△ADB(SAS),
∴∠ABE=∠ACE,
∴∠BEC=180° - ∠ACE - ∠EAC - ∠AEB=180° - ∠ABE - ∠EAC - ∠AEB=∠BAC=90°. ②作AG⊥BE于点G,如答图①所示.

∵△AEC≌△ADB,
∴BD=EC=3.
∵F为AC的中点,
∴AF=CF.在△AGF和△CEF中,∠AFG=∠CFE,∠AGF=∠CEF,AF=CF,
∴△AGF≌△CEF(AAS),
∴AG=EC=3,
∴S△ACE=S△ADB=1/2×3×3 = 4.5.
∵F为AC的中点,
∴S△AEF=1/2S△ACE=1/2×4.5 = 2.25.
(3)解:连接EC,如答图②所示.

∵∠BAC=∠ADE=90°,CD⊥DF,
∴∠CDE=∠FDA.在△CDE和△FDA中,CD=FD,∠CDE=∠FDA,DE=DA,
∴△CDE≌△FDA(SAS),
∴CE=AF,∠DCE=∠AFD.
∵DC=DF,CD⊥DF,
∴△CDF为等腰直角三角形,
∴∠DCF=∠CFD=45°,
∴∠AFD=180° - 45° = 135°,
∴∠DCE=∠AFD=135°,
∴∠ECA=135° - 45° = 90°,
∴∠ACE=∠BAC=90°,
∴CE//AB,
∴S△ACE=S△FCB.
∵△CEF是公共部分,
∴S△AEF=S△CFB=18.设AF的长度为a,则S△AEF=a²/2 = 18,解得a = 6(负值已舍去),故AF的长为6.
查看更多完整答案,请扫码查看


