《2025年全品学练考九年级数学上册人教版》

1. (2024 安徽)若扇形OAB的半径为6,$∠AOB=$ $120^{\circ }$,则$\widehat {AB}$的长为 (C)
A. $2π$
B. $3π$
C. $4π$
D. $6π$

答案： C

2. (2024 青岛)如图24-4-1,A,B,C,D是$\odot O$上的点,半径$OA=3,\widehat {AB}=\widehat {CD},∠DBC=25^{\circ },$连接AD,则扇形OAB的面积为 (A)
A. $\frac {5}{4}π$
B. $\frac {5}{8}π$
C. $\frac {5}{2}π$
D. $\frac {5}{12}π$

答案： A

3. 如图24-4-2,在$Rt△ABC$中,$∠ACB=90^{\circ },$ $AB=\sqrt {5},BC=2$,以点A为圆心,AC的长为半径画弧,交AB于点D,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为 (D)
A. $8-π$
B. $4-π$
C. $2-\frac {π}{4}$
D. $1-\frac {π}{4}$

答案： D

4. (2023 永州)已知扇形的半径为6,面积为$6π,$ 则扇形圆心角的度数为$ 60 ^ { \circ } $.

答案： $ 60 ^ { \circ } $

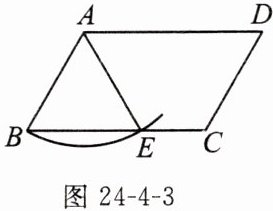
5. (2024 镇江)如图24-4-3,四边形ABCD为平行四边形,以点A为圆心,AB长为半径画弧,交BC边于点E,连接AE.若$AB=1,∠D=60^{\circ }$,则$\widehat {BE}$的长$l=$$\frac { 1 } { 3 } \pi$(结果保留π).

答案： $ \frac { 1 } { 3 } \pi $

6. (2023 青岛)如图24-4-4,四边形ABCD是$\odot O$的内接四边形,$∠B=58^{\circ },∠ACD=40^{\circ }.$若$\odot O$的半径为5,则$\widehat {DC}$的长为 (C)
A. $\frac {13}{3}π$
B. $\frac {10}{9}π$
C. $π$
D. $\frac {1}{2}π$

答案： C

7. (2024 兰州)“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图24-4-5①是陈列在展览馆的仿真模型,图②是模型驱动部分的示意图,其中$\odot M,\odot N$的半径分别是1 cm和10 cm,当$\odot M$顺时针转动3周时,$\odot N$上的点P随之旋转$n^{\circ }$,则$n=$108.

答案： 108

8. 如图24-4-6所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在$\widehat {AD}$上,$∠BAC=22.5^{\circ }$,则$\widehat {BC}$的长为 $\frac {5\pi}{4}$.

答案： $ \frac { 5 \pi } { 4 } $

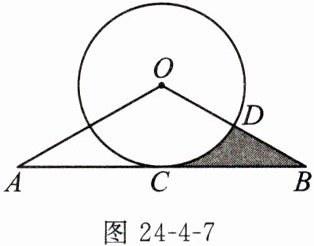
9. (2024 青海)如图24-4-7,直线AB经过点C,且$OA=OB,CA=CB,\odot O$交直线AB于点C.
(1)求证:直线AB是$\odot O$的切线;
(2)若圆的半径为4,$∠B=30^{\circ }$,求阴影部分的面积.

答案：
(1) 证明: 连接 $ OC $.
$ \because OA = OB $, $ CA = CB $, $ \therefore OC \perp AB $.
又 $ \because OC $ 是 $ \odot O $ 的半径,
$ \therefore $ 直线 $ AB $ 是 $ \odot O $ 的切线.
(2) $ 8 \sqrt { 3 } - \frac { 8 \pi } { 3 } $