第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
11. 如图24-1-6,OA是⊙O的半径,B为OA上一点(点B不与点O,A重合),过点B作OA的垂线交⊙O于点C,以OB,BC为边作矩形OBCD.若CD=6,BC=8,则AB的长为 (
A. 6
B. 5
C. 4
D. 2
C
)A. 6
B. 5
C. 4
D. 2
答案:
C
12. 如图24-1-7,A,B,C是⊙O上的三点,∠AOB=50°,∠OBC=40°,则∠OAC的度数为 (
A. 10°
B. 15°
C. 20°
D. 25°
B
)A. 10°
B. 15°
C. 20°
D. 25°
答案:
B
13. 如图24-1-8,AB是⊙O的直径,点D,C在⊙O上,AD//OC,∠DAB=60°,连接AC,则∠DAC=
30
°.
答案:
30
14. (教材习题24.1T13变式)如图24-1-9,四边形ABCO是菱形,点A,B,C在⊙O上,若⊙O的半径是6,求弦AC的长.
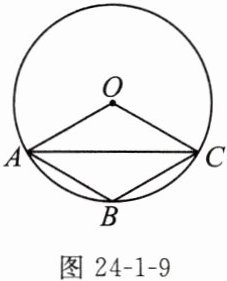

答案:
$6\sqrt{3}$
15. 如图24-1-10,⊙O的直径AB与弦CD的延长线交于点E.若DE=OB,∠AOC=87°,求∠E的度数.


答案:
$29^{\circ}$
16. 核心素养创新意识课本上将绳子的一端系一支笔,另一端固定,将绳子绷直,用笔绕着另一端画一圈就是一个圆,于是我们定义:圆是所有到定点的距离等于定长的点的集合.
下面是一种画椭圆的方法:
(1)在地面上选两个点,钉上两个钉子;
(2)测量两个钉子间的距离;
(3)选用大于两钉子间距离长度的绳子;
(4)将绳子的两端分别系在钉子上;
(5)将绳子绷直,用笔在绷直的拐角地方画线;
(6)将绳子绕一圈,椭圆就得到啦!(如图24-1-11所示)
请你根据这个过程给椭圆下一个定义:
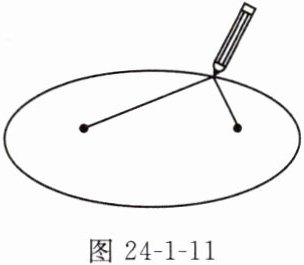
下面是一种画椭圆的方法:
(1)在地面上选两个点,钉上两个钉子;
(2)测量两个钉子间的距离;
(3)选用大于两钉子间距离长度的绳子;
(4)将绳子的两端分别系在钉子上;
(5)将绳子绷直,用笔在绷直的拐角地方画线;
(6)将绳子绕一圈,椭圆就得到啦!(如图24-1-11所示)
请你根据这个过程给椭圆下一个定义:
平面内与两个定点的距离的和等于常数(大于两定点间的距离)的点的轨迹叫做椭圆
.
答案:
平面内与两个定点的距离的和等于常数(大于两定点间的距离)的点的轨迹叫做椭圆
查看更多完整答案,请扫码查看


