《2025年全品学练考九年级数学上册人教版》

3.如图7-ZT-6,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且$∠EDF=$$45^{\circ }$,将$△DAE$绕点D逆时针旋转$90^{\circ }$,得到$△DCM.$
(1)求证:$EF=MF;$
(2)当$AE=1$时,求EF的长.

答案：
(1)证明:
∵将△DAE绕点D逆时针旋转90°,得到△DCM,
∴DM=DE,∠EDM=90°.
∵∠EDF=45°,
∴∠MDF=45°,
∴∠EDF=∠MDF.
在△DEF和△DMF中,
∴△DEF≌△DMF,
∴EF=MF.
$(2)\frac { 5 } { 2 }$

4.观察猜想
(1)如图7-ZT-7①,在$Rt△ABC$中,$∠BAC=$$90^{\circ },AB=AC$,D为BC边上一动点,且不与点B重合,连接AD,将$△ABD$绕点A逆时针旋转$90^{\circ }$,得到$△ACE$,那么CE,BD之间的位置关系为____,数量关系为____;
数学思考
(2)如图②,在$Rt△ABC$中,$∠BAC=90^{\circ },$$AB=AC$,D,E为BC上两点,且$∠DAE=$$45^{\circ }$.求证:$BD^{2}+CE^{2}=DE^{2};$
拓展延伸
(3)如图③,在$△ABC$中,$∠BAC=120^{\circ },AB=$$AC,∠DAE=60^{\circ }$,若以BD,DE,EC为边的三角形是以BD为斜边的直角三角形,当$BD=2$时,求DE的长.

答案：
解:
(1)CE⊥BD CE=BD
(2)证明:如图①,把△ACE绕点A顺时针旋转90°,得到△ABG,连接DG.
∵∠BAC=90°,AB=AC,
∴∠ABC=∠C=45°.
由旋转的性质可知AG=AE,BG=CE,∠ABG=∠C=45°,∠GAE=90°,
∴∠DAG=∠GAE−∠DAE=45°,
∴∠DAG=∠DAE.
在△ADG和△ADE中,
$\left\{ \begin{array} { l } { A G = A E, } \\ { \angle D A G = \angle D A E, } \\ { A D = A D, } \end{array} \right.$
∴△ADG≌△ADE(SAS),
∴DG=DE.
∵∠GBD=∠ABG+∠ABC=90°,
∴BD²+BG²=DG²,
即BD²+CE²=DE².
(3)如图②,将△AEC绕点A顺时针旋转120°,得到△AFB,连接DF.

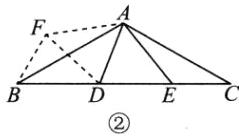
由旋转的性质可知AF=AE,∠ABF=∠C,EC=BF,∠FAE=120°.
又
∵∠DAE=60°,
∴∠DAF=∠FAE−∠DAE=60°,
∴∠DAE=∠DAF.
在△ADE和△ADF中,
$\left\{ \begin{array} { l } { A D = A D, } \\ { \angle D A E = \angle D A F, } \\ { A E = A F, } \end{array} \right.$
∴△ADE≌△ADF(SAS),
∴DE=DF.
∵∠BAC=120°,AB=AC,
∴∠ABC=∠C=30°,
∴∠ABF=30°,
∴∠FBD=60°.
∵以BD,DE,EC为边的三角形是以BD为斜边的直角三角形,
∴以BD,DF,BF为边的三角形是以BD为斜边的直角三角形,
∴△BDF是直角三角形,且∠BFD=90°,
∴∠BDF=30°,
∴BD=2BF=2,
∴BF=1,
∴DF=$\sqrt { BD^2 - BF^2} = \sqrt { 3 }$,
∴DE=$\sqrt { 3 }$.