《2025年全品学练考九年级数学上册人教版》

8. 如图21-3-9，某小区计划在一个长16m，宽9m的矩形场地ABCD内修建若干条同样宽的小路，使竖直的小路与AB平行，水平的小路与AD平行，其余部分种草.已知草坪部分的总面积为$ 112m^{2} $.设小路的宽为xm，若x满足方程$ x^{2} - 17x + 16 = 0 $，则修建小路的示意图是 (C)

答案： C

9. 如图21-3-10，利用一面墙(墙长25米)，用总长度为49米的栅栏(图中实线部分)围成一个矩形围栏ABCD，且中间留两个1米宽的小门，设BC的长为x米.
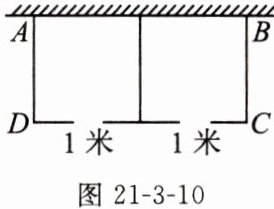
(1)若矩形围栏ABCD的面积为210平方米，求BC的长.
(2)矩形围栏ABCD的面积能否为240平方米？若能，求出相应的x的值；若不能，请说明理由.

答案： 解：由$BC = x$米，可知$AB = (49 + 1 + 1 - 3x) = (51 - 3x)$米.
(1)依题意，得$x(51 - 3x) = 210$，
整理，得$x^{2} - 17x + 70 = 0$，
解得$x_{1} = 7$，$x_{2} = 10$.
当$x = 7$时，$51 - 3x = 51 - 3×7 = 30 ＞ 25$，不合题意，舍去；
当$x = 10$时，$51 - 3x = 51 - 3×10 = 21 ＜ 25$，符合题意.
答：BC的长为10米.
(2)矩形围栏ABCD的面积不能为240平方米.
理由如下：
假设矩形围栏ABCD的面积为240平方米，则$x(51 - 3x) = 240$，
整理，得$x^{2} - 17x + 80 = 0$.
$\because \Delta = (-17)^{2} - 4×1×80 = -31 ＜ 0$，
∴此方程无实数根，
∴矩形围栏ABCD的面积不能为240平方米.

10. 已知：如图21-3-11，在$ \triangle ABC $中，$ \angle B = 90^{\circ} $，$ AB = 5cm $，$ BC = 7cm $.点P从点A开始沿AB边向点B以1cm/s的速度匀速运动，同时点Q从点B开始沿BC边向点C以2cm/s的速度匀速运动.当其中一点到达终点时，另一点也随之停止运动.设运动时间为$ x s(x ＞ 0) $.
(1)1s后，$ \triangle PBQ $的面积为$ 4cm^{2} $；
(2)几秒后，PQ的长度为5cm？
解：在$Rt\triangle PBQ$中，由勾股定理，得$BP^{2} + BQ^{2} = PQ^{2}$，即$(5 - x)^{2} + (2x)^{2} = 5^{2}$，整理，得$x^{2} - 2x = 0$，解得$x_{1} = 0$（不合题意，舍去），$x_{2} = 2$.答：2s后，PQ的长度为5cm.
(3)$ \triangle PBQ $的面积能否为$ 7cm^{2} $？请说明理由.
解：不能. 理由：假设$\triangle PBQ$的面积为$7cm^{2}$，则由题意，得$\frac{1}{2}(5 - x)·2x = 7$，整理，得$x^{2} - 5x + 7 = 0$.$\because \Delta = b^{2} - 4ac = (-5)^{2} - 4×1×7 = 25 - 28 = -3 ＜ 0$，∴此方程无实数根，$\therefore \triangle PBQ$的面积不能为$7cm^{2}$.

答案： 解：由题意，得$AP = xcm$，$BP = (5 - x)cm$，$BQ = 2xcm$.
(1)1
(2)在$Rt\triangle PBQ$中，由勾股定理，得$BP^{2} + BQ^{2} = PQ^{2}$，
即$(5 - x)^{2} + (2x)^{2} = 5^{2}$，
整理，得$x^{2} - 2x = 0$，
解得$x_{1} = 0$（不合题意，舍去），$x_{2} = 2$.
答：2s后，PQ的长度为5cm.
(3)不能. 理由：假设$\triangle PBQ$的面积为$7cm^{2}$，
则由题意，得$\frac{1}{2}(5 - x)·2x = 7$，
整理，得$x^{2} - 5x + 7 = 0$.
$\because \Delta = b^{2} - 4ac = (-5)^{2} - 4×1×7 = 25 - 28 = -3 ＜ 0$，
∴此方程无实数根，
$\therefore \triangle PBQ$的面积不能为$7cm^{2}$.