《2025年点石成金金牌每课通七年级数学上册人教版辽宁专版》

5 如图，用边长是1的小正方形组成网格，第1个网格中有$1×1$个小正方形，所有线段的和是4；第2个网格中有$2×2$个小正方形，所有线段的和是12；第3个网格中有$3×3$个小正方形，所有线段的和是24……按此规律，第$n$个网格中所有线段的和是______$2n(n + 1)$.

答案： $2n(n + 1)$
解析
根据所给图形可知，
第1个网格中所有线段的和是 $2×1×2 = 4$；
第2个网格中所有线段的和是 $2×2×3 = 12$；
第3个网格中所有线段的和是 $2×3×4 = 24$；
……
所以第n个网格中所有线段的和是 $2n×(n + 1)$.

6 如图，用若干根相同的小木棒拼图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……按此规律，拼第20个图形需要158根小木棒.

答案： 158
解析
根据所给图形可知，
拼第1个图形需要小木棒6根；
拼第2个图形需要小木棒 $6×2 + 2 = 14$ (根)；
拼第3个图形需要小木棒 $6×3 + 2×2 = 22$ (根)；
……
所以拼第n个图形需要小木棒 $[6n + 2×(n - 1)]$ 根.
所以当 $n = 20$ 时，
$6n + 2(n - 1) = 158$ (根).

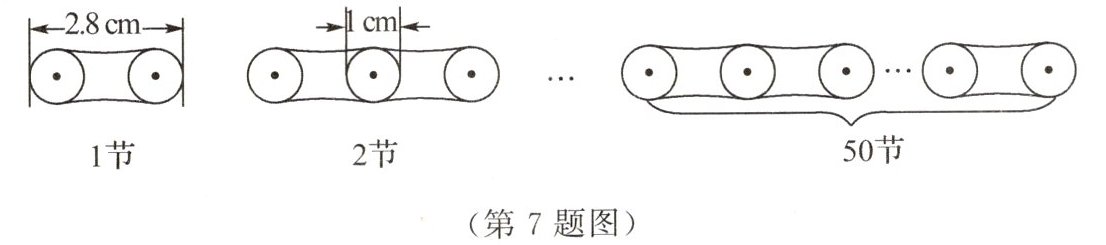
7 如图，某链条每节长为2.8cm，每两节链条相连接部分重叠的圆的直径是1cm，按这种连接方式，50节链条的总长度是91cm.

答案： 91
解析
由所给图形可知，
1节链条的长度是 $2.8cm$；
2节链条的总长度是 $2.8 + (2.8 - 1) = 4.6$ (cm)；
3节链条的总长度是 $2.8 + (2.8 - 1)×2 = 6.4$ (cm)；
……
所以n节链条的总长度是 $2.8 + (2.8 - 1)×(n - 1) = [2.8 + 1.8(n - 1)]$ cm.
所以当 $n = 50$ 时，
$2.8 + 1.8(n - 1) = 91$ (cm).

8 我们将按如图1和图2所示的方式排列的点的个数分别称作“三角形数”（如1，3，6，10，…）和“正方形数”（如1，4，9，16，…），在小于100的数中，设最大的“三角形数”是$x$，最大的“正方形数”是$y$，则$x + y$的值是______172.

答案： 172
解析
因为“三角形数”分别是 $1,3,6,10,\cdots$，
所以第m个“三角形数” $x = \frac{m(m + 1)}{2}$.
因为 $x ＜ 100$，且m是正整数，
所以m的最大值是13.
当 $m = 13$ 时， $x = \frac{13×(13 + 1)}{2} = 91$.
因为“正方形数”分别是 $1,4,9,16,\cdots$，
所以第n个“正方形数” $y = n^2$.
因为 $y ＜ 100$，且n是正整数，
所以n的最大值是9.
当 $n = 9$ 时， $y = 9^2 = 81$.
所以 $x + y = 91 + 81 = 172$.

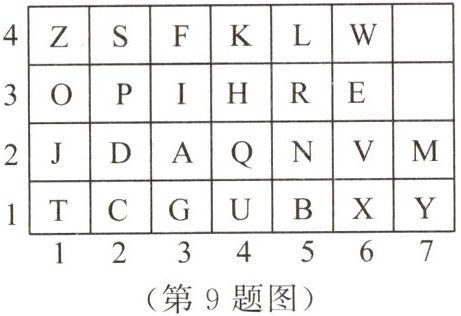
9 数学活动课上，老师和同学们用如图所示的密码表玩听声音猜动物的游戏.当听到“叮叮—叮，叮叮—叮叮，叮—叮”时，分别对应的字母是“C，A，T”，表示的动物是猫.当听到“叮叮—叮，叮—叮叮叮，叮叮叮叮叮—叮叮叮叮”时，表示的动物是（A）

A. 奶牛
B. 蜜蜂
C. 狗
D. 猪

答案： 9. A

10 在密码学中，把可以直接看到的内容称为明码，把对明码进行某种处理后得到的内容称为密码.有一种密码，将26个英文字母$a$，$b$，$c$，…，$z$依次对应1，2，3，…，26这26个自然数.当明码对应的数$x$是奇数时，密码对应的数$y = \frac{x + 1}{2}$；当明码对应的数$x$是偶数时，密码对应的数$y = \frac{x}{2} + 13$.按该规定，将明码“yano”译成密码是math.（密码是字母）

答案： math