《2025年启东中学作业本八年级数学上册江苏版》

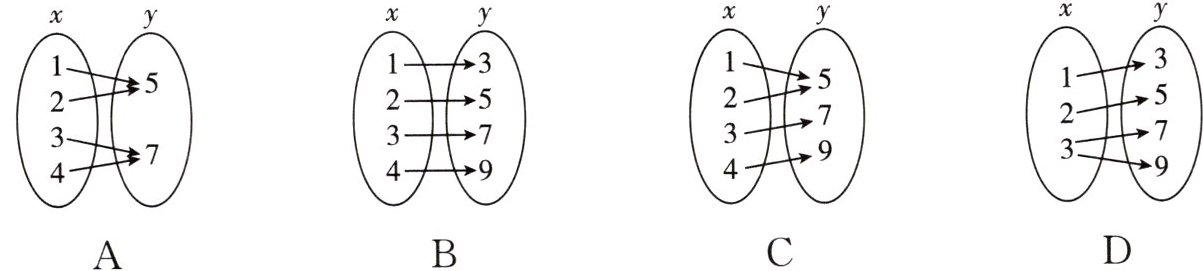
8. 下列关于变量 x,y 的关系,其中 y 不是 x 的函数的是 (D)

答案： D

9. 如图,在长方形 ABCD 中,$AB = 5,AD = 3$,点 P 从点 A 出发,沿长方形 ABCD 的边逆时针运动,设点 P 运动的距离为 x,$△APC$的面积为 y,如果$5 ＜ x ＜ 8$,那么 y 关于 x 的函数关系式为$ y = -\frac{5}{2}x + 20 $.

答案： $ y = -\frac{5}{2}x + 20 $

10. 物理实验证实:在弹性限度内,某弹簧长度 y(cm)与所挂物体质量 x(kg)满足函数关系式$y = kx + 15$. 下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
| x/kg | 0 | 2 | 5 |
| --- | --- | --- | --- |
| y/cm | 15 | 19 | 25 |
(1)求 y 与 x 的函数关系式;
(2)当弹簧长度为 20 cm 时,求所挂物体的质量.

答案： 解：
(1) 把 $ x = 2 $，$ y = 19 $ 代入 $ y = kx + 15 $ 中，
得 $ 19 = 2k + 15 $，解得 $ k = 2 $，
所以 $ y $ 与 $ x $ 的函数关系式为 $ y = 2x + 15(x≥0) $。
(2) 把 $ y = 20 $ 代入 $ y = 2x + 15 $ 中，得 $ 20 = 2x + 15 $，
解得 $ x = 2.5 $。
故所挂物体的质量为 2.5 kg。

11. 观察如图所示图形,解答问题.
(1)若第 n(n 为正整数,从上往下数)行白球与黑球的总数记作 y,求 y 与 n 的函数关系式;
(2)求第 2025 行白球和黑球的总数.
(1)y=3n - 1
(2)6074

答案： 解：
(1) 第 $ n $ 行白球数为 $ n $，黑球数为 $ 2n - 1 $，
所以 $ y $ 与 $ n $ 的函数关系式为 $ y = n + 2n - 1 $，即 $ y = 3n - 1 $。
(2) 第 2025 行白球和黑球的总数为 $ 3×2025 - 1 = 6074 $。

12. 如图,正方形 ABCD 的边长为 4 cm,E,F 分别是 BC,CD 边上的动点,点 E,F 同时从点 C 出发,以每秒 2 cm 的速度分别向点 B,D 运动,当点 E 与点 B 重合时,运动停止. 设运动时间为 x s,运动过程中$△AEF$的面积为$ycm^{2}$,求 y 关于 x 的函数关系式,并写出自变量 x 的取值范围.

$y=$$-2x^2 + 8x$($0 ＜ x ≤ 2$)

答案： 解：
∵ 点 $ E $，$ F $ 同时从点 $ C $ 出发，以每秒 2 cm 的速度分别向点 $ B $，$ D $ 运动，
∴ $ CE = 2x $ cm，$ CF = 2x $ cm，$ BE = (4 - 2x) $ cm，$ DF = (4 - 2x) $ cm，
∴ $ S_{△AEF} = S_{正方形 ABCD} - S_{△ABE} - S_{△ADF} - S_{△ECF} = 16 - \frac{1}{2}×AB×BE - \frac{1}{2}×AD×DF - \frac{1}{2}×EC×FC = 16 - \frac{1}{2}×4×(4 - 2x) - \frac{1}{2}×4×(4 - 2x) - \frac{1}{2}×2x×2x = -2x^2 + 8x $，
即 $ y = -2x^2 + 8x(0 ＜ x ≤ 2) $。