第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 如图所示,人的头部、颈椎和颈部肌肉可当成一个杠杆(支
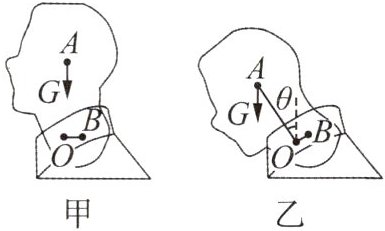
点在颈椎O处)。当头颅为竖直状态时,颈部肌肉的拉力为零,当低下时,颈部肌肉会产生一定的拉力,A点为头颅模型的重心,B点为肌肉拉力的作用点,拉力的方向始终垂直于OB。低头过程中,重力的力臂逐渐____,拉力逐渐____。所以长时间低头会产生疲劳。(均选填“增大”“减小”或“不变”)

点在颈椎O处)。当头颅为竖直状态时,颈部肌肉的拉力为零,当低下时,颈部肌肉会产生一定的拉力,A点为头颅模型的重心,B点为肌肉拉力的作用点,拉力的方向始终垂直于OB。低头过程中,重力的力臂逐渐____,拉力逐渐____。所以长时间低头会产生疲劳。(均选填“增大”“减小”或“不变”)
答案:
增大 增大 解析:由题意和图示可知,低头过程中,支点O到重力作用线的距离变大,则头颅重力的力臂增大;阻力臂增大,阻力G、拉力的力臂不变,根据杠杆的平衡条件可知,拉力会增大.
变式1 动力方向保持与杠杆垂直
2. (2025·江苏南通期末)如图所示,在轻质杠杆最右端挂一重物,最左端施加一个始终与杠杆垂直的力F。若不考虑杠杆的摩擦阻力,将杠杆从水平位置(如图实线部分所示)缓慢匀速转到图示虚线位置过程中,拉力F大小()

A. 逐渐变小
B. 逐渐变大
C. 保持不变
D. 先变大再变小
2. (2025·江苏南通期末)如图所示,在轻质杠杆最右端挂一重物,最左端施加一个始终与杠杆垂直的力F。若不考虑杠杆的摩擦阻力,将杠杆从水平位置(如图实线部分所示)缓慢匀速转到图示虚线位置过程中,拉力F大小()

A. 逐渐变小
B. 逐渐变大
C. 保持不变
D. 先变大再变小
答案:
A 解析:由题意知,动力始终垂直于杠杆,则动力臂不变,杠杆转动到虚线位置过程中,阻力G 始终竖直向下且大小不变,阻力臂变小,根据杠杆的平衡条件可知,在此过程中拉力F逐渐变小,故A正确.
方法归纳
力F始终与杠杆垂直,如图所示

杠杆在转动过程中,l不变,$l_{G}$先变大再变小,G不变,由$Fl=Gl_{G}$可知,F先变大后变小.
A 解析:由题意知,动力始终垂直于杠杆,则动力臂不变,杠杆转动到虚线位置过程中,阻力G 始终竖直向下且大小不变,阻力臂变小,根据杠杆的平衡条件可知,在此过程中拉力F逐渐变小,故A正确.
方法归纳
力F始终与杠杆垂直,如图所示

杠杆在转动过程中,l不变,$l_{G}$先变大再变小,G不变,由$Fl=Gl_{G}$可知,F先变大后变小.
变式2 动力方向水平不变
3. (2025·江苏苏州期中)如图所示,一根可绕O点转动的均匀硬棒重为G,在棒的一端始终施加水平力F,将棒从图示位置缓慢提起至虚线位置的过程中()
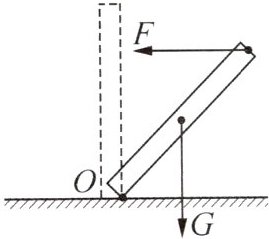
A. F的力臂变小,F变大
B. F的力臂变大,F变小
C. 重力G与它的力臂的乘积保持不变
D. 重力G与它的力臂的乘积变大
3. (2025·江苏苏州期中)如图所示,一根可绕O点转动的均匀硬棒重为G,在棒的一端始终施加水平力F,将棒从图示位置缓慢提起至虚线位置的过程中()

A. F的力臂变小,F变大
B. F的力臂变大,F变小
C. 重力G与它的力臂的乘积保持不变
D. 重力G与它的力臂的乘积变大
答案:
B
方法归纳
力F始终在水平方向上,如图所示

杠杆由图示位置转至水平位置时,$l_{G}$变大,l变小,由$Fl=Gl_{G}$可知,F变大.
B
方法归纳
力F始终在水平方向上,如图所示

杠杆由图示位置转至水平位置时,$l_{G}$变大,l变小,由$Fl=Gl_{G}$可知,F变大.
变式3 动力方向竖直不变
4. (2025·江苏徐州质检)如图所示,轻质杠杆OA中点悬挂重为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是____N;保持F的方向始终竖直,将杠杆从OA位置匀速提升到OB位置的过程中,力F的大小将____(选填“变大”“变小”或“不变”)。
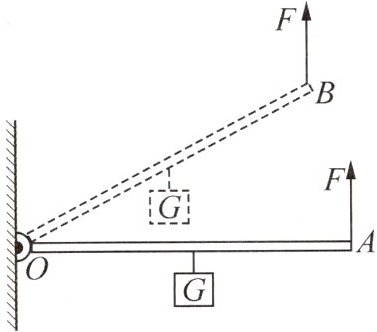
4. (2025·江苏徐州质检)如图所示,轻质杠杆OA中点悬挂重为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是____N;保持F的方向始终竖直,将杠杆从OA位置匀速提升到OB位置的过程中,力F的大小将____(选填“变大”“变小”或“不变”)。

答案:
30 不变 解析:如图,设杠杆的中点在C(D)处,则$L_{OA}=2L_{OC}$、$L_{OB}=2L_{OD}$.杠杆在OA位置(水平位置)时,由杠杆的平衡条件可得$FL_{OA}=GL_{OC}$,则$F=\frac {GL_{OC}}{L_{OA}}=\frac {1}{2}G=\frac {1}{2}×60N=30N$.将杠杆从OA位置匀速提升到OB位置过程中,$OA'$为动力臂,$OC'$为阻力臂,阻力不变为G,由数学知识可得,$\frac {L_{OC'}}{L_{OA'}}=\frac {L_{OD}}{L_{OB}}=\frac {1}{2}$,由杠杆的平衡条件得$F'L_{OA'}=GL_{OC'}$,则$F'=\frac {GL_{OC'}}{L_{OA'}}=\frac {1}{2}G=\frac {1}{2}×60N=30N$.由此可知,当杠杆从OA位置匀速提升到OB位置的过程中,力F的大小将不变.

方法归纳
力F始终在竖直方向上,如图所示

由杠杆平衡条件知$Fl=Gl_{G}$,则$F=G\frac {l_{G}}{l}$,又因为$\triangle OCD$相似于$\triangle OBA$,所以$\frac {l_{G}}{l}=\frac {OD}{OA}$,即$\frac {l_{G}}{l}$是一个定值,G大小不变,所以F也是一个定值,即F大小不变.
30 不变 解析:如图,设杠杆的中点在C(D)处,则$L_{OA}=2L_{OC}$、$L_{OB}=2L_{OD}$.杠杆在OA位置(水平位置)时,由杠杆的平衡条件可得$FL_{OA}=GL_{OC}$,则$F=\frac {GL_{OC}}{L_{OA}}=\frac {1}{2}G=\frac {1}{2}×60N=30N$.将杠杆从OA位置匀速提升到OB位置过程中,$OA'$为动力臂,$OC'$为阻力臂,阻力不变为G,由数学知识可得,$\frac {L_{OC'}}{L_{OA'}}=\frac {L_{OD}}{L_{OB}}=\frac {1}{2}$,由杠杆的平衡条件得$F'L_{OA'}=GL_{OC'}$,则$F'=\frac {GL_{OC'}}{L_{OA'}}=\frac {1}{2}G=\frac {1}{2}×60N=30N$.由此可知,当杠杆从OA位置匀速提升到OB位置的过程中,力F的大小将不变.

方法归纳
力F始终在竖直方向上,如图所示

由杠杆平衡条件知$Fl=Gl_{G}$,则$F=G\frac {l_{G}}{l}$,又因为$\triangle OCD$相似于$\triangle OBA$,所以$\frac {l_{G}}{l}=\frac {OD}{OA}$,即$\frac {l_{G}}{l}$是一个定值,G大小不变,所以F也是一个定值,即F大小不变.
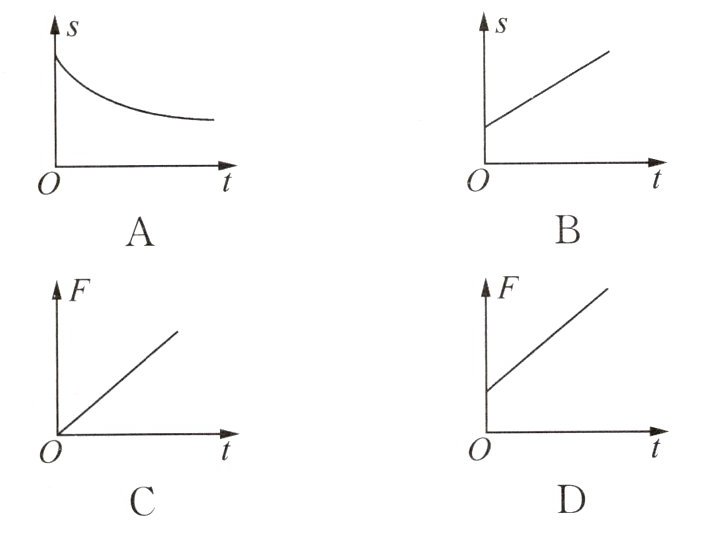
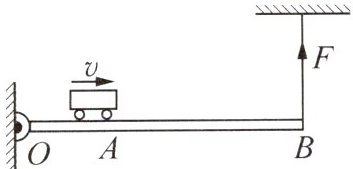
5. 如图,小车从处于轻质杠杆OB的A点开始匀速向右运动,在B端竖直向上方向系一根不可伸缩的细绳使杠杆始终处于水平位置平衡。下列表示AB间的距离s和细绳的拉力F随时间t变化的关系图线中,可能正确的是()


答案:
D 解析:由题意可得AB间的距离$s=OB-(OA+vt)=OB - OA - vt$,由于OB、OA是定值,小车速度v不变,则s随t的增大而减小,且是一次函数关系,故A、B错误;杠杆始终处于水平位置平衡,根据杠杆的平衡条件可知$F×OB=G×(OA + vt)$,则$F=\frac {G×OA}{OB}+\frac {Gv}{OB}t$,可知F和t为一次函数关系,由于小车从A点开始运动,所以t = 0时细绳的拉力F不为零,故C 错误、D正确.
查看更多完整答案,请扫码查看


