《2025年亮点给力提优课时作业本九年级物理上册苏科版》

1. 如图甲所示的电路中,当开关S闭合后,电压表$V_{1}和V_{2}$的示数均如图乙所示,则灯$L_{1}$、$L_{2}$两端的电压不可能是 ()

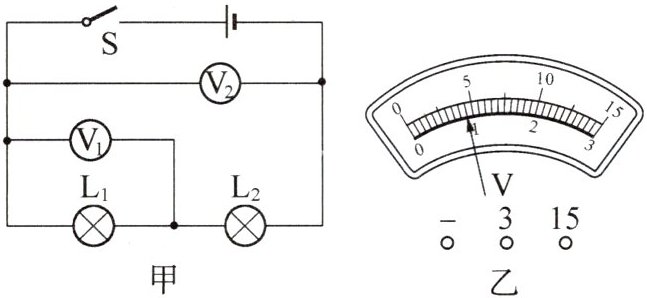
A. 0.9 V 3.6 V
B. 0.9 V 0 V
C. 4.5 V 0 V
D. 4.5 V 4.5 V

答案： D 解析：由图甲可知，两灯串联，电压表 $ V_{2} $ 测电源电压，电压表 $ V_{1} $ 测灯 $ L_{1} $ 两端的电压. 若电路无故障，因为串联电路中总电压等于各部分电路两端电压之和，且 $ V_{1} $、$ V_{2} $ 的偏转角度相同，所以电压表 $ V_{1} $ 的量程为 $ 0 \sim 3 \mathrm{V} $、$ V_{2} $ 的量程为 $ 0 \sim 15 \mathrm{V} $，由图乙知 $ V_{2} $ 的示数为 $ 4.5 \mathrm{V} $，则电源电压 $ U = 4.5 \mathrm{V} $，灯 $ L_{1} $ 两端的电压 $ U_{1} = 0.9 \mathrm{V} $，所以灯 $ L_{2} $ 两端的电压 $ U_{2} = U - U_{1} = 4.5 \mathrm{V} - 0.9 \mathrm{V} = 3.6 \mathrm{V} $，故 A 可能；若灯 $ L_{2} $ 短路，则灯 $ L_{2} $ 两端的电压为 $ 0 \mathrm{V} $，$ V_{1} $ 和 $ V_{2} $ 均测灯 $ L_{1} $ 两端的电压，即电源电压，两电压表示数相同，若 $ V_{1} $ 和 $ V_{2} $ 的量程都是 $ 0 \sim 3 \mathrm{V} $，则灯 $ L_{1} $、$ L_{2} $ 两端的电压是 $ 0.9 \mathrm{V} $、$ 0 \mathrm{V} $，若 $ V_{1} $ 和 $ V_{2} $ 的量程都是 $ 0 \sim 15 \mathrm{V} $，则灯 $ L_{1} $、$ L_{2} $ 两端的电压是 $ 4.5 \mathrm{V} $、$ 0 \mathrm{V} $，故 B、C 可能；无论两个电压表所用的量程是否相同，灯 $ L_{1} $、$ L_{2} $ 两端的电压都不可能相等，故 D 不可能.

2. 新趋势 综合实践 (2025·江苏南京期中)创新小组同学制作“硬币”电池,具体步骤如下.① 剪纸:将吸水纸和锡箔纸剪成与五角硬币大小相同的形状;② 垒电池:按锡箔纸、吸水纸(用醋浸泡过)的顺序叠放,组成一枚“硬币”,将这样的“硬币”一层一层地叠加;③ 连接:将两根导线分别连接在“硬币”电池的上下两面,将LED灯接入电路,LED灯即可发光.为了检测“硬币”电池的正负极,小组同学用导线将一个电流表和一个开关串联在“硬币”电池的吸水纸和锡箔纸两端,然后______,如果出现______的现象,可得出与电流表正接线柱相连的一端为“硬币”电池的正极.

答案： 闭合开关并迅速断开 电流表指针正向偏转 解析：用导线将“硬币”电池、电流表和开关组成串联电路，检查电路连接准确后，闭合开关并迅速断开，观察电流表指针的偏转方向. 在闭合开关瞬间，若电流表指针正向偏转，则与正接线柱相连的一端为“硬币”电池的正极，反之为“硬币”电池的负极.

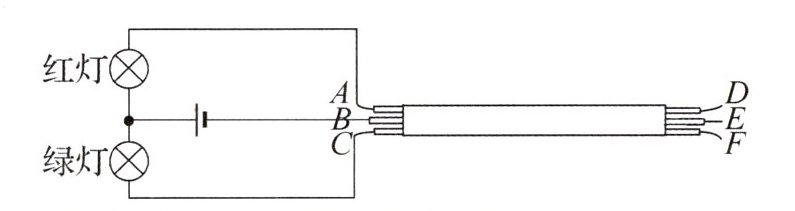
3. 如图所示,在一根横跨河流两岸的硬塑料管内穿有三根完全相同的电线,为了辨别哪两个线头为同一根导线的两端,可以用图示方法测试,其操作过程如下:用两个颜色不同的小灯泡接入电路,分别用导线连接D、E、F,记录观察到的现象如表所示,就可判断出所有导线的首尾.则A和______为一根导线;B和______为一根导线.

答案： $ E $ $ F $ 解析：由图及表中信息可知，连接 $ D $、$ E $，小灯泡全不亮，说明 $ D $、$ E $ 没有与 $ B $ 连通而形成通路，故 $ B $ 不与 $ D $、$ E $ 相连；连接 $ D $、$ F $，绿灯亮，说明 $ D $、$ F $ 与 $ B $、$ C $ 连通形成通路，即它们一定是其中两根导线的线头，则剩下的 $ A $ 和 $ E $ 一定为一根导线；连接 $ E $、$ F $，红灯亮，说明 $ E $、$ F $ 与 $ A $、$ B $ 连通形成通路，同理，它们一定是其中两根导线的线头，则剩下的 $ C $ 和 $ D $ 一定为一根导线. 由此可知，$ B $ 和 $ F $ 为一根导线.

4. 如图,当开关S闭合后,通过$L_{2}$的电流方

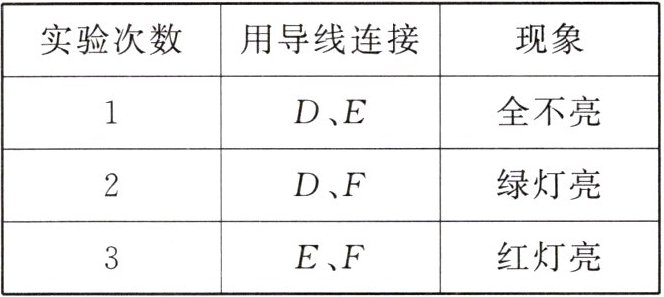
向为______(选填“向左”或“向右”);$A_{2}$的示数为3 A,$A_{3}$的示数为1 A,交换某两个灯泡后,再次闭合开关,$A_{2}$、$A_{3}$的示数均不变,则$A_{1}$的示数为______A.

答案： 向左 $ 3.5 $ 解析：由图可知，三个灯泡并联，电流有三条路径，其中一条路径电流从电源的正极出发，依次经过 $ A_{1} $、$ A_{2} $、$ L_{2} $、$ A_{3} $ 回到电源的负极，所以通过 $ L_{2} $ 的电流方向为向左. 电流表 $ A_{1} $ 测干路电流、$ A_{2} $ 测通过 $ L_{2} $ 和 $ L_{3} $ 的总电流、$ A_{3} $ 测通过 $ L_{1} $ 和 $ L_{2} $ 的总电流. 设通过 $ L_{1} $、$ L_{2} $、$ L_{3} $ 的电流分别为 $ I_{1} $、$ I_{2} $、$ I_{3} $，因为并联电路中干路电流等于各支路电流之和，所以 $ I_{2} + I_{3} = 3 \mathrm{A} $、$ I_{1} + I_{2} = 1 \mathrm{A} $；交换某两个灯泡后，再次闭合开关，
答案详解精析
$ A_{2} $、$ A_{3} $ 的示数均不变，说明互换的两个灯泡中通过的电流相等. 若互换的灯泡为 $ L_{2} $ 和 $ L_{1} $，则 $ I_{1} = I_{2} = \frac{1}{2} \times 1 \mathrm{A} = 0.5 \mathrm{A} $、$ I_{3} = 3 \mathrm{A} - 0.5 \mathrm{A} = 2.5 \mathrm{A} $，此时电流表 $ A_{1} $ 的示数 $ I = I_{1} + I_{2} + I_{3} = 0.5 \mathrm{A} + 0.5 \mathrm{A} + 2.5 \mathrm{A} = 3.5 \mathrm{A} $；若互换的灯泡为 $ L_{2} $ 和 $ L_{3} $，则 $ I_{2} = I_{3} = \frac{1}{2} \times 3 \mathrm{A} = 1.5 \mathrm{A} $、$ I_{1} = 1 \mathrm{A} - 1.5 \mathrm{A} = - 0.5 \mathrm{A} $，这种情况不会出现；若互换的灯泡为 $ L_{1} $ 和 $ L_{3} $，则 $ I_{1} = I_{3} $，由并联电路的电流规律可知，电流表 $ A_{2} $ 和电流表 $ A_{3} $ 的示数相等，不符合题意. 综上所述，电流表 $ A_{1} $ 的示数为 $ 3.5 \mathrm{A} $.

5. 新素养 科学思维 一辆卡车驾驶室内的灯,由左右两道门上的开关$S_{1}$、$S_{2}和车内司机右上方的开关S_{3}$共同控制.$S_{1}和S_{2}$分别由左右两道门的开、关来控制:门打开后,$S_{1}和S_{2}$闭合;门关上后,$S_{1}和S_{2}$断开.$S_{3}$是一个单刀三掷开关,根据需要可将其置于三个不同位置.请设计一个电路,要求在三个开关的共同控制下,分别具有如下三个功能:(1)无论门开还是关,灯都不亮.(2)打开两道门中的任意一道或两道都打开时,灯亮;两道门都关上时,灯不亮.(3)无论门开还是关,灯都亮.请在如图所示的方框中画出电路图.

答案：
如图所示