《2025年亮点给力提优课时作业本九年级物理上册苏科版》

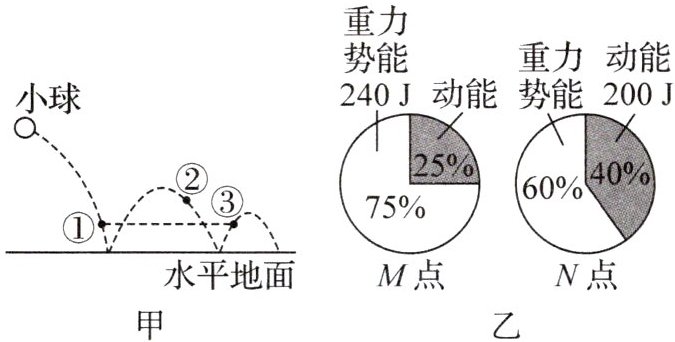
1. (2025·江苏苏州期中)某小球被水平抛出后,其部分运动轨迹如图甲,其中位置①和③离地高度相等,小球在运动过程中经过M、N两点,其动能和重力势能的参数如图乙,且M、N两点分别为图中“①”“②”或“③”点中的两点,则小球 ()

A. 经过的M点就是点②
B. 在点③的速度比在点②大
C. 在M点的重力势能大于在N点的
D. 在点①的动能大于260J

答案： D 解析：由图乙可知，小球在M点时的机械能$E_{M}=\frac{240J}{75\%}=320J$，动能$E_{M动}=E_{M}-E_{M势}=320J - 240J = 80J$，小球在N点时的机械能$E_{N}=\frac{200J}{40\%}=500J$，重力势能$E_{N势}=E_{N}-E_{N动}=500J - 200J = 300J$，可知小球在N点时的机械能大于在M点时的机械能，且在N点时重力势能较大，而小球在运动过程中，机械能不断减小，且位置①和③离地高度相等，小球在此两点时重力势能相等，所以N点对应的是②，M点对应的是③，在M点的重力势能小于在N点的，故A、C不符合题意；由以上分析可知，小球在点③的动能80J比在点②的动能200J小，所以小球在点③的速度比在点②小，故B不符合题意；小球在点①时的重力势能与在点③时的重力势能相等，为240J，小球在运动过程中，机械能不断减小，所以小球在点①时的机械能大于在点②时的机械能500J，即$E＞500J$，$E_{势}=240J$，则它在点①的动能$E_{动}=E - E_{势}＞500J - 240J = 260J$，所以小球在点①的动能大于260J，故D符合题意。

2. 汽车出厂前需要测试,某次测试过程中,汽车保持恒定功率在水平路面做直线运动,其v-t图像如图所示.汽车运动过程中受到的阻力不变,发动机效率为40%,加速至2s时牵引力为4000N,10s后油箱还剩10L汽油(汽油的热值$q= 3.3×10^7J/L),$则汽车的功率为______kW.运动中汽车受到的阻力为______N,10s后该车最多还能继续行驶的路程为______km.

答案： 60 2000 66 解析：由题意可知，汽车的功率保持不变，且加速至2s时，牵引力为4000N.由图可知，当加速至2s时，汽车的速度为15m/s，则汽车的功率$P = F_{牵}v = 4000N×15m/s = 60000W = 60kW$.由图可知，当汽车运动到10s时，汽车开始做匀速直线运动，其速度为30m/s，此时牵引力和阻力是一对平衡力，大小相等.所以汽车受到的阻力$f = F_{牵}'=\frac{P}{v'}=\frac{60000W}{30m/s}=2000N$.由题意可知，10s后还剩10L的汽油，10L汽油完全燃烧所释放的热量$Q_{放}=Vq = 10L×3.3×10^{7}J/L = 3.3×10^{8}J$，利用剩下的10L汽油，汽车最多能做的有用功$W = ηQ_{放}=40\%×3.3×10^{8}J = 1.32×10^{8}J$，汽车最多还能行驶的路程$s=\frac{W}{F_{牵}'}=\frac{1.32×10^{8}J}{2000N}=6.6×10^{4}m = 66km$.

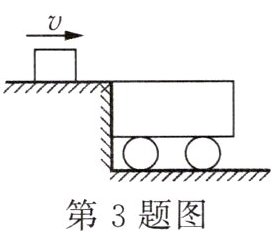
3. 新素养 科学思维 (2025·江苏南京月考)已知物体的动能表达式为$E_{k}= \frac {1}{2}mv^{2}$,其中m为物体的质量,v为物体的运动速度.如图所示,质量m_1= 8kg的平顶小车静止在光滑的水平轨道上,车顶与左侧光滑平台等高,平台上放置质量m_2= 2kg的小物块,小物块以5m/s的初速度向右运动,滑上小车.最终小物块静止在小车上,并以1m/s的速度与小车一起向右运动.若此过程中机械能全部转化为内能且全部被小物块吸收,则小物块内能增大了______J,能使小物块的温度升高______℃.[小物块的比热容为2×10^3J/(kg·℃)]

答案： 20 $5×10^{-3}$ 解析：小物块初始的动能$E_{k1}=\frac{1}{2}m_{2}v_{1}^{2}=\frac{1}{2}×2kg×(5m/s)^{2}=25J$，小物块最终的动能$E_{k2}=\frac{1}{2}m_{2}v_{2}^{2}=\frac{1}{2}×2kg×(1m/s)^{2}=1J$，因为原来小车速度为零，所以原来小车的动能也为零，小车动能的增加量$E_{k3}=\frac{1}{2}m_{1}v_{2}^{2}=\frac{1}{2}×8kg×(1m/s)^{2}=4J$，小物块增加的内能$Q_{吸}=E_{k1}-E_{k2}-E_{k3}=25J - 1J - 4J = 20J$，由$Q_{吸}=cmΔt$可得，小物块升高的温度$Δt=\frac{Q_{吸}}{cm_{2}}=\frac{20J}{2×10^{3}J/(kg·^{\circ}C)×2kg}=5×10^{-3}^{\circ}C$.

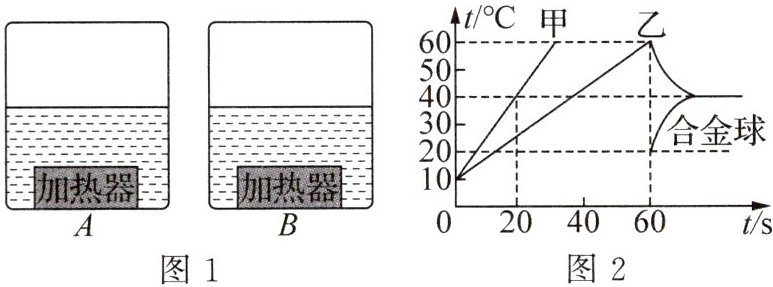
4. (2025·湖北黄石期中)如图1,A、B是两个底部装有完全相同的加热器的容器,加热器产生热量的90%可以被容器中的液体吸收,已知加热器每秒钟放出热量1000J.现将甲、乙两种液体分别倒入A、B两容器中,其中甲液体的比热容为$2×10^3J/(kg·℃);$让两个加热器同时开始工作,60s后停止加热,然后立即将质量为2.7kg的合金球迅速放入乙液体中(从球放入到达到热平衡不计热损失),它们的温度随时间变化的图像如图2所示.求:

(1) 加热20s时,乙液体吸收的热量为多少?
(2) 甲液体的质量为多少?
(3) 合金球的比热容为多少?

答案：
(1) $1.8×10^{4}J$
(2) 0.3kg
(3) $0.4×10^{3}J/(kg·^{\circ}C)$ 解析：
(1) 已知加热器每秒钟放出热量1000J，则加热20s时，加热器放出热量$Q_{放}=1000J/s×20s = 2×10^{4}J$，由题意可知，乙液体吸收的热量$Q_{乙吸}=Q_{放}×90\% = 2×10^{4}J×90\% = 1.8×10^{4}J$.
(2) 由题意可知，A、B两容器底部装有完全相同的加热器，则甲液体在20s内吸收的热量等于乙液体20s内吸收的热量，即$Q_{甲吸}=Q_{乙吸}=1.8×10^{4}J$，加热20s时，甲液体的温度从10°C升高到40°C，由$Q_{吸}=cm(t - t_{0})$可得，甲液体的质量$m_{甲}=\frac{Q_{甲吸}}{c_{甲}(t - t_{0})}=\frac{1.8×10^{4}J}{2×10^{3}J/(kg·^{\circ}C)×(40^{\circ}C - 10^{\circ}C)}=0.3kg$.
(3) 由图2可知，加热60s时，乙液体的温度从10°C升高到60°C，则加热60s乙液体升高的温度$Δt_{乙升}=60^{\circ}C - 10^{\circ}C = 50^{\circ}C$，加热60s乙液体吸收的热量$Q_{乙吸}'=c_{乙}m_{乙}Δt_{乙升}$，加热20s时乙液体吸收的热量$Q_{乙吸}=1.8×10^{4}J$，则加热60s时乙液体吸收的热量$Q_{乙吸}'=3Q_{乙吸}=3×1.8×10^{4}J = 5.4×10^{4}J$，合金球放入乙液体后，乙液体的温度从60°C降低到40°C，则乙液体放热时降低的温度$Δt_{乙降}=60^{\circ}C - 40^{\circ}C = 20^{\circ}C$，合金球放入乙液体后，乙液体放出的热量$Q_{乙放}=c_{乙}m_{乙}Δt_{乙降}$，则两过程中乙液体放出的热量与其吸收的热量的比值$\frac{Q_{乙放}}{Q_{乙吸}'}=\frac{c_{乙}m_{乙}Δt_{乙降}}{c_{乙}m_{乙}Δt_{乙升}}=\frac{Δt_{乙降}}{Δt_{乙升}}=\frac{20^{\circ}C}{50^{\circ}C}=\frac{2}{5}$，所以$Q_{乙放}=\frac{2}{5}Q_{乙吸}'=\frac{2}{5}×5.4×10^{4}J = 2.16×10^{4}J$，从球放入到达到热平衡不计热损失，则$Q_{球吸}=Q_{乙放}=2.16×10^{4}J$，由图2可知，合金球放入乙液体后，合金球的温度从20°C升高到40°C，则合金球升高的温度$Δt_{球升}=40^{\circ}C - 20^{\circ}C = 20^{\circ}C$，由$Q_{吸}=cmΔt$可得，合金球的比热容$c_{球}=\frac{Q_{球吸}}{m_{球}Δt_{球升}}=\frac{2.16×10^{4}J}{2.7kg×20^{\circ}C}=0.4×10^{3}J/(kg·^{\circ}C)$.