《2025年亮点给力提优课时作业本九年级物理上册苏科版》

1. (2025·福建厦门期中)甲、乙两物体的比热容之比为2:3,乙的质量是甲的两倍,若它们吸收相等的热量,则甲、乙两物体升高温度之比为 ()
A. 3:4
B. 4:3
C. 1:3
D. 3:1

答案： D 解析：由题意可知，甲、乙两物体的比热容之比 $ c_{甲}:c_{乙}=2:3 $，乙的质量是甲的两倍，则 $ m_{甲}:m_{乙}=1:2 $，若它们吸收相等的热量，即 $ Q_{甲}:Q_{乙}=1:1 $，由 $ Q_{吸}=cm\Delta t $ 可得， $ \Delta t=\frac{Q_{吸}}{cm} $，则甲、乙两物体升高温度之比 $ \frac{\Delta t_{甲}}{\Delta t_{乙}}=\frac{\frac{Q_{甲}}{c_{甲}m_{甲}}}{\frac{Q_{乙}}{c_{乙}m_{乙}}}=\frac{Q_{甲}}{Q_{乙}}\times\frac{c_{乙}}{c_{甲}}\times\frac{m_{乙}}{m_{甲}}=\frac{1}{1}\times\frac{3}{2}\times\frac{2}{1}=\frac{3}{1} $，故 D 正确。

2. 亮点原创·周末,小明在家跟妈妈学习煲汤.假设小明所煲汤的质量为2kg、初温为20℃,不计热量损失,在标准大气压下,要使汤沸腾,汤需要吸收______J的热量.[汤的比热容$c_{汤}= 4.2×10^{3}J/(kg\cdot ^{\circ }C)$,汤的沸点视为水的沸点]

答案： $ 6.72\times10^{5} $ 解析：汤的沸点视为水的沸点，标准大气压下水的沸点为 $ 100^{\circ}C $，则汤沸腾时的温度为 $ 100^{\circ}C $，不计热量损失，要使汤沸腾，汤需要吸收的热量 $ Q_{吸}=c_{汤}m\Delta t=4.2\times10^{3}J/(kg\cdot^{\circ}C)\times2kg\times(100^{\circ}C - 20^{\circ}C)=6.72\times10^{5}J $。

3. 一个质量为500g的钢件,先将其加热到520℃,然后放在室温为20℃的环境中让其自然冷却.可知该钢件在冷却的过程中所释放的热量为______J.如果这些热量被质量为1kg、初温为30℃的水吸收,最多能使水的温度升高到______℃.[$c_{钢}= 0.46×10^{3}J/(kg\cdot ^{\circ }C),c_{水}= 4.2×10^{3}J/(kg\cdot ^{\circ }C)$,结果保留一位小数]

答案： $ 1.15\times10^{5} $ $ 57.4 $ 解析：该钢件在冷却过程中所释放的热量 $ Q_{放}=c_{钢}m_{钢}(t_{0}-t)=0.46\times10^{3}J/(kg\cdot^{\circ}C)\times500\times10^{-3}kg\times(520^{\circ}C - 20^{\circ}C)=1.15\times10^{5}J $。由题意可知，水吸收的热量 $ Q_{吸}=Q_{放}=1.15\times10^{5}J $，由 $ Q_{吸}=cm(t_{2}-t_{1}) $ 可知，水的末温 $ t_{2}=\frac{Q_{吸}}{c_{水}m_{水}}+t_{1}=\frac{1.15\times10^{5}J}{4.2\times10^{3}J/(kg\cdot^{\circ}C)\times1kg}+30^{\circ}C\approx57.4^{\circ}C $。

4. 新教材 半个多世纪以来,三代塞罕坝林场人艰苦奋斗、甘于奉献,以坚韧不拔的斗志和永不言败的担当,建设了百万亩人工林海.塞罕坝林场不仅是守卫京津的重要生态屏障,而且可以调节气温,营造“宜居无为”的舒适环境.请你结合比热容的知识,解释塞罕坝林场可以调节气温的原因.

答案： 植树造林能涵养水源、保持水土，水的比热容大，由 $ Q=cm\Delta t $ 可知，在质量一定、吸收或放出相同热量时，水的温度变化小，所以塞罕坝林场可以调节气温。

5. 铁的比热容大于铜的比热容.质量相等的铁球和铜球放入开水中很长一段时间,如果将它们拿出,释放相同的热量后相互接触,热传递的情况是 ()
A. 铜球传给铁球
B. 铁球传给铜球
C. 不进行热传递
D. 不确定

答案： B 解析： $ c_{铁}＞c_{铜} $，质量、初温相同的铜球和铁球放出相同的热量后，由 $ Q_{放}=cm\Delta t $ 可知，铜球的温度降低得多；因为铁球和铜球的初温相同，所以铜球的末温低，因此两球接触后热量从铁球传给铜球。故 B 正确。

6. 不计热量损失,若将一杯质量为300g的热水倒入容器内的冷水中,冷水温度升高10℃,又向容器内倒入同样一杯热水,冷水温度又升高6℃.若再向容器内倒入同样一杯热水,则下列说法正确的是()
A. 冷水温度升高3℃
B. 一开始冷水和热水的温差为40℃
C. 一开始容器内冷水的质量为150g
D. 一开始容器内冷水的质量为450g

答案： B 解析：设一开始热水和冷水的温度差为 $ t $，将质量为 $ m_{0} $ 的热水倒入质量为 $ m $ 的冷水中，使得冷水温度升高了 $ 10^{\circ}C $，不计热量损失， $ Q_{放}=Q_{吸} $，可得 $ cm_{0}(t - 10^{\circ}C)=cm\times10^{\circ}C $ ①，又倒入同样一杯热水，冷水温度又升高了 $ 6^{\circ}C $，可得 $ cm_{0}(t - 10^{\circ}C - 6^{\circ}C)=c(m + m_{0})\times6^{\circ}C $ ②，则 ① - ② 可得 $ m = 3m_{0}=3\times300g = 900g $，代入 ① 可得， $ t = 40^{\circ}C $；若将三杯热水一次性注入，可得 $ 3cm_{0}(40^{\circ}C - \Delta t)=cm\Delta t $ ③，将 $ m = 3m_{0} $ 代入，解得 $ \Delta t = 20^{\circ}C $，则注入第 3 杯热水后，冷水温度还会上升 $ 20^{\circ}C - 10^{\circ}C - 6^{\circ}C = 4^{\circ}C $，综上所述，B 正确。
### 易错警示
本题考查了热平衡方程的应用，解题时注意三杯热水分次倒入与一次性倒入效果是相同的。

7. (2025·山东济南期中)糖炒栗子是人们钟爱的一道传统美食,如图所示,为了让栗子快速、均匀受热,常将砂石与栗子混合在一起翻炒,这主要是利用了砂石的______,相同质量的栗子和砂石吸收相同的热量,砂石的温度升高得更______.

答案： 比热容小 多

8. (2025·河南郑州月考)用稳定的热源给一个0.5kg的物体均匀加热,得到它的熔化图像如图所示,已知该物体在固态时的比热容为$0.2×10^3J/(kg·℃),$由此可得该物体在BC段熔化过程中吸收的热量为______J;则该物质在液态时的比热容为______J/(kg·℃).

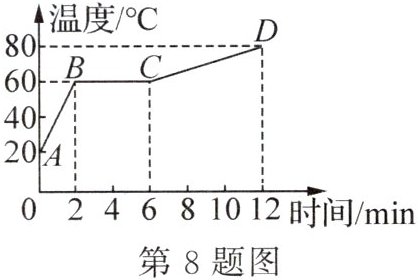
答案： $ 8\times10^{3} $ $ 1.2\times10^{3} $ 解析： $ AB $ 段吸收的热量 $ Q_{AB}=c_{固}m(t - t_{0})=0.2\times10^{3}J/(kg\cdot^{\circ}C)\times0.5kg\times(60^{\circ}C - 20^{\circ}C)=4\times10^{3}J $，稳定的热源相同时间内供热相同，物体吸热相同，则该物体在 $ BC $ 段吸收的热量是 $ AB $ 段吸收热量的 2 倍，即 $ Q_{BC}=2Q_{AB}=2\times4\times10^{3}J = 8\times10^{3}J $；由图可知， $ AB $ 段物质为固态， $ CD $ 段为液态，质量不变， $ AB $ 段物质温度升高 $ 40^{\circ}C $， $ CD $ 段物质温度升高 $ 20^{\circ}C $，温度升高之比 $ \Delta t_{固}:\Delta t_{液}=2:1 $， $ CD $ 段加热时间是 $ AB $ 段加热时间的 3 倍，即吸收热量之比 $ Q_{固}:Q_{液}=1:3 $，则该物质固态与液态比热容之比 $ \frac{c_{固}}{c_{液}}=\frac{\frac{Q_{固}}{m\Delta t_{固}}}{\frac{Q_{液}}{m\Delta t_{液}}}=\frac{Q_{固}}{Q_{液}}\frac{\Delta t_{液}}{\Delta t_{固}}=\frac{1\times1}{3\times2}=\frac{1}{6} $，所以该物质液态时的比热容 $ c_{液}=6c_{固}=6\times0.2\times10^{3}J/(kg\cdot^{\circ}C)=1.2\times10^{3}J/(kg\cdot^{\circ}C) $。